题目内容
阅读下面材料:
| 如图(15),圆的概念:在平面内,线段PA绕它固定的一个端点P旋转一周,另一个端点A所形成的图形叫做圆. 就是说,到某个定点等于定长的所有点在同一个圆上. 圆心在 如:圆心在 (1)填空: ①以 ②以 (2)根据以上材料解决以下问题:
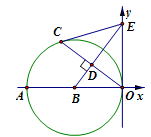
如图(16),以 | |
①连接EC,证明EC是⊙B的切线;
②在BE上是否存在一点P,使PB=PC=PE=PO,若存在,求P点坐标,并写出以P为圆心,以PB为半径的⊙P的方程;若不存在,说明理由.
解:(1)①方程为:
②方程为:
(2)①证明
∵OB=BC BD⊥OC
∴∠OBD=∠CBD
∵BE=BE
∴△BOE≌△BCE
∵AO⊥OE
∴∠BCE=∠BOE=900
∴EC是⊙B的切线
| ②存在 取BE的中点P连接PC、PO ∵△BCE和△B ∴PC= ∴PC=PB=PO=PE 过P作PM⊥ ∵P是BE中点 ∴OM= ∵∠AOC+∠EOC=900 ∠BEO+∠EOC=900 ∴∠AOC=∠BEO ∴
由勾股定理:
∴⊙P的方程为 |
|
|
|

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案下面的多项式在实数范围内能因式分解的是( )
|
| A. | x2+y2 | B. | x2﹣y | C. | x2+x+1 | D. | x2﹣2x+1 |
如图(5),E是矩形ABCD中BC边的中点,将△ABE沿AE折叠到△AEF,F在矩形ABCD内部,延长AF交DC于G点,若∠AEB=550,
∠DAF的度数?

|
如图,OA⊥OB,若∠1=55°,则∠2的度数是( )
|
 ,半径为
,半径为 的圆的方程可以写为:
的圆的方程可以写为: .
. ,半径为5的圆的方程为:
,半径为5的圆的方程为: .
. 为圆心, 1为半径的圆的方程为:
为圆心, 1为半径的圆的方程为:  ;
; 为圆心,
为圆心,  为半径的圆的方程为: ;
为半径的圆的方程为: ;
 为圆心的圆与
为圆心的圆与 轴相切于原点,C是⊙B上一点,连接OC,作BD⊥OC垂足为D,延长BD交
轴相切于原点,C是⊙B上一点,连接OC,作BD⊥OC垂足为D,延长BD交 .
. BE PO=
BE PO= 轴于M、PN⊥
轴于M、PN⊥
 ,即
,即 ∴BE=10
∴BE=10
 ,
,




 ,OA=4,AB=5,点D在反比例函数
,OA=4,AB=5,点D在反比例函数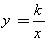 (k>0)的图象上,
(k>0)的图象上,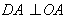 ,点P在y轴负半
,点P在y轴负半 轴上,OP=7.
轴上,OP=7.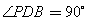 时,求反比例函数的解析式
时,求反比例函数的解析式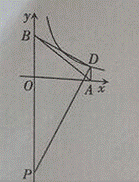

 A.(
A.( )n·75° B.(
)n·75° B.(
