题目内容
13．已知a，b，c为三角形的三边长，且满足（6a+8b+10c）-（a2+b2+c2）=50，则该三角形的形状为（ ）| A． | 等腰三角形 | B． | 等边三角形 | C． | 直角三角形 | D． | 等腰直角三角形 |
分析 利用一次项的系数分别求出常数项，把50分成9、16、25，然后与（a2-6a）、（b2-8b）、（c2-10c）分别组成完全平方公式，再利用非负数的性质，可分别求出a、b、c的值，然后利用勾股定理可证△ABC实直角三角形．
解答 解：∵（6a+8b+10c）-（a2+b2+c2）=50，
∴a2-6a+9+b2-8b+16+c2-10c+25=0，
即（a-3）2+（b-4）2+（c-5）2=0，
∴a=3，b=4，c=5，
∵32+42=52，
∴△ABC是直角三角形．
故选C．
点评 本题考查了配方法的应用、勾股定理、非负数的性质，解题的关键是注意配方法的步骤，在变形的过程中不要改变式子的值．
练习册系列答案
相关题目
如图，在△ABC中，∠B=∠C，点D是BC边的中点，若∠BAD=35°，则∠DAC=35°．
1．a，b，c为三个有理数，下列各式可写成a-b+c的是（ ）
| A． | a-（-b）-（+c） | B． | a-（+b）-（-c） | C． | a+（-b）+（-c） | D． | a+（-b）-（+c） |
18．画△ABC中BC边上的高，下面的画法中，正确的是（ ）
| A． |  | B． |  | C． |  | D． |  |
2．
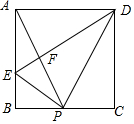如图，在矩形ABCD中，P是BC上一点，E是AB上一点，PD平分∠APC，PE⊥PD，连接DE交AP于F，在以下判断中，不正确的是（ ）
如图，在矩形ABCD中，P是BC上一点，E是AB上一点，PD平分∠APC，PE⊥PD，连接DE交AP于F，在以下判断中，不正确的是（ ）| A． | 当P为BC中点，△APD是等边三角形 | B． | 当△ADE∽△BPE时，P为BC中点 | ||
| C． | 当AE=2BE时，AP⊥DE | D． | 当△APD是等边三角形时，BE+CD=DE |
