题目内容
如图，已知半径OD与弦AB互相垂直，垂足为点C，若AB=8cm，CD=3cm，则圆O的半径为（ ）A．
cmB．5cm
C．4cm
D．
cm
【答案】分析：连接AO，根据垂径定理可知AC=
AB=4cm，设半径为x，则OC=x-3，根据勾股定理即可求得x的值．
解答：解：连接AO，
∵半径OD与弦AB互相垂直，
∴AC=
AB=4cm，
设半径为x，则OC=x-3，
在Rt△ACO中，AO2=AC2+OC2，
即x2=42+（x-3）2，
解得：x=
，
故半径为
cm．
故选A．
点评：本题考查了垂径定理及勾股定理的知识，解答本题的关键是熟练掌握垂径定理、勾股定理的内容，难度一般．
AB=4cm，设半径为x，则OC=x-3，根据勾股定理即可求得x的值．解答：解：连接AO，
∵半径OD与弦AB互相垂直，
∴AC=
AB=4cm，设半径为x，则OC=x-3，
在Rt△ACO中，AO2=AC2+OC2，
即x2=42+（x-3）2，
解得：x=
，故半径为
cm．故选A．
点评：本题考查了垂径定理及勾股定理的知识，解答本题的关键是熟练掌握垂径定理、勾股定理的内容，难度一般．
练习册系列答案
相关题目
（2013•广安）如图，已知半径OD与弦AB互相垂直，垂足为点C，若AB=8cm，CD=3cm，则圆O的半径为（ ）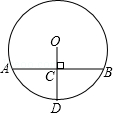
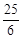cm B．5cm C．4cm D．
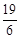cm
如图，已知半径OD与弦AB互相垂直，垂足为点C，若AB=8cm，CD=3cm，则圆O的半径为
cm
cm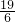如图，已知半径OD与弦AB互相垂直，垂足为点C，若AB=8cm，CD=3cm，则圆O的半径为（ ）
|
| A． |
| B． | 5cm | C． | 4cm | D． |
|
cm
cm