题目内容
【题目】某种蔬菜的销售单价y1与销售月份x之间的关系如图(1)所示,成本y2与销售月份之间的关系如图(2)所示(图(1)的图象是线段图(2)的图象是抛物线)
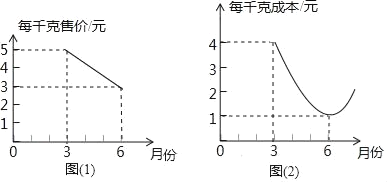
(1)分别求出y1、y2的函数关系式(不写自变量取值范围);
(2)通过计算说明:哪个月出售这种蔬菜,每千克的收益最大?
【答案】(1)y1=![]() ;y2=
;y2=![]() x2﹣4x+13;(2)5月出售每千克收益最大,最大为
x2﹣4x+13;(2)5月出售每千克收益最大,最大为![]() .
.
【解析】
(1)观察图象找出点的坐标,利用待定系数法即可求出y1和y2的解析式;
(2)由收益W=y1-y2列出W与x的函数关系式,利用配方求出二次函数的最大值.
解:(1)设y1=kx+b,将(3,5)和(6,3)代入得,![]() ,解得
,解得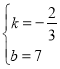 .
.
∴y1=﹣![]() x+7.
x+7.
设y2=a(x﹣6)2+1,把(3,4)代入得,
4=a(3﹣6)2+1,解得a=![]() .
.
∴y2=![]() (x﹣6)2+1,即y2=
(x﹣6)2+1,即y2=![]() x2﹣4x+13.
x2﹣4x+13.
(2)收益W=y1﹣y2,
=﹣![]() x+7﹣(
x+7﹣(![]() x2﹣4x+13)
x2﹣4x+13)
=﹣![]() (x﹣5)2+
(x﹣5)2+![]() ,
,
∵a=﹣![]() <0,
<0,
∴当x=5时,W最大值=![]() .
.
故5月出售每千克收益最大,最大为![]() 元.
元.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
【题目】二次函数![]() =ax2+bx+c的部分对应值如表,利用二次的数的图象可知,当函数值y>0时,x的取值范围是( )
=ax2+bx+c的部分对应值如表,利用二次的数的图象可知,当函数值y>0时,x的取值范围是( )
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 |
y | ﹣12 | ﹣5 | 0 | 3 | 4 | 3 |
A.0<x<2B.x<0或x>2C.﹣1<x<3D.x<﹣1或x>3