题目内容
下列方程的解分别是:(1)
| x-1 |
| x+1 |
| 2x |
| 1-x2 |
(2)
| x+3 |
| x2-3x+2 |
| x+2 |
| x2-4x+3 |
| x+1 |
| x2-5x+6 |
(3)2(x+
| 1 |
| x |
| 1 |
| x |
(4)x2+2x-
| 3 |
| x2+2x+1 |
(5)
| 1 |
| x2-2x-1 |
| 2 |
| x2-2x-2 |
| 3 |
| x2-2x-3 |
(6)
| 1 |
| x-1 |
| 1 |
| x-2 |
| 1 |
| x-6 |
| 1 |
| x-7 |
(7)
| x-8 |
| x-10 |
| x-4 |
| x-6 |
| x-5 |
| x-7 |
| x-7 |
| x-9 |
分析:这几道题应注意换元法的运用;解决此类题如
+
=
+
,关键是使其分母先相等或分子先相等,再使其分子或分母相等.
| x-8 |
| x-10 |
| x-4 |
| x-6 |
| x-5 |
| x-7 |
| x-7 |
| x-9 |
解答:解:(1)∵
-
=0,∴(x-1)2-2x=0,
∴x2-4x+1=0,x1=2+
,x2=2-
;
2)∵
+
=
,
∴(x+3)(x-3)+(x+2)(x-2)=(x+1)(x-1),
∴x2=12,∴x1=2
,x2=-2
.
(3)令y=x+
,则原方程化为2y2-3y-5=0,
∴y1=-1,y2=
,∴x+
=-1,x2+x+1=0无解,或x+
=
,
∴2x2-5x+2=0,∴x1=2,x2=
;
(4)令x2+2x-1=y,则原方程化为y-
=2,∴y2-2y-3=0,∴y1=3,y2=-1,∴x2-2x-1=3,即x2-2x-4=0,∴x1=
-1,x2=-
-1
或x2+2x-1=-1,∴x3=0,x4=-2.
(5)设x2-2x-1=y,则原方程化为
+
=
∴(y-1)(y-2)+2y(y-2)-3y(y-1)=0,∴4y-2=0,y=
,∴x2-2x-1=
,∴2x2-4x-3=0,
∴x1=
,x2=
.
(6)∵
=
,
∴
=
∴10x=40,∴x=4.
(7)
+
=
+
∴原方程化为
-
=
+
∴
-
=
-
∴
=
∴x=8.
| x-1 |
| x+1 |
| 2x |
| (x+1)(x-1) |
∴x2-4x+1=0,x1=2+
| 3 |
| 3 |
2)∵
| x+3 |
| (x-1)(x-2) |
| (x+2) |
| (x-1)(x-3) |
| x+1 |
| (x-2)(x-3) |
∴(x+3)(x-3)+(x+2)(x-2)=(x+1)(x-1),
∴x2=12,∴x1=2
| 3 |
| 3 |
(3)令y=x+
| 1 |
| x |
∴y1=-1,y2=
| 5 |
| 2 |
| 1 |
| x |
| 1 |
| x |
| 5 |
| 2 |
∴2x2-5x+2=0,∴x1=2,x2=
| 1 |
| 2 |
(4)令x2+2x-1=y,则原方程化为y-
| 3 |
| y |
| 5 |
| 5 |
或x2+2x-1=-1,∴x3=0,x4=-2.
(5)设x2-2x-1=y,则原方程化为
| 1 |
| y |
| 2 |
| y-1 |
| 3 |
| y-2 |
∴(y-1)(y-2)+2y(y-2)-3y(y-1)=0,∴4y-2=0,y=
| 1 |
| 2 |
| 1 |
| 2 |
∴x1=
2+
| ||
| 2 |
2-
| ||
| 2 |
(6)∵
| (x-2)-(x-1) |
| (x-2)(x-1) |
| (x-7)-(x-6) |
| (x-6)(x-7) |
∴
| 1 |
| (x-2)(x-1) |
| 1 |
| (x-6)(x-7) |
∴10x=40,∴x=4.
(7)
| x-10+2 |
| x-10 |
| x-6+2 |
| x-6 |
| x-7+2 |
| x-7 |
| x-6+2 |
| x-9 |
∴原方程化为
| 1 |
| x-10 |
| 1 |
| x-6 |
| 1 |
| x-7 |
| 1 |
| x-9 |
∴
| 1 |
| x-10 |
| 1 |
| x-9 |
| 1 |
| x-7 |
| 1 |
| x-6 |
∴
| 1 |
| (x-10)(x-9) |
| 1 |
| (x-7)(x-6) |
点评:本题主要考查用换元法解分式方程,难度较大.注意:换元法应先将方程中多次出现的一个式子设为一个字母,然后得到一个新的方程,然后解出,反代入原式即可求解.

练习册系列答案
相关题目
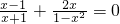 ______.
______.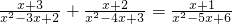 ______.
______.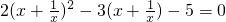 ______.
______.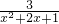 =2______.
=2______.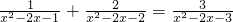 ______.
______.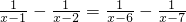 ______.
______.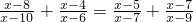 ______.
______.