题目内容
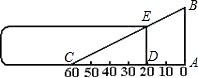
某校计划在一块三角形的空地上修建一个面积最大的正方形水池，使得水池的一边在△ABC的边BC上，△ABC中边BC=60m，高AD=30m，则水池的边长应为（ ）
| A．10m | B．20m | C．30m | D．40m |
如图：设水池的边长为xm
∵四边形EFGH是正方形
∴EF∥BC
∴△AEF∽△ABC
∴
=
∴（30-x）：30=x：60
∴x=20m
∴水池的边长应为20m．
故选B．
∵四边形EFGH是正方形∴EF∥BC
∴△AEF∽△ABC
∴
| AM |
| AD |
| EF |
| BC |
∴（30-x）：30=x：60
∴x=20m
∴水池的边长应为20m．
故选B．
练习册系列答案
相关题目
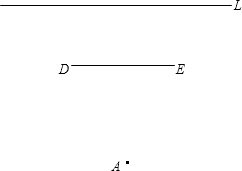路的巨型广告牌（DE）．广告牌挡住了小华的视线