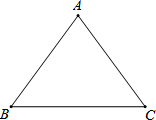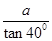题目内容
如图，在△ABC中，∠C=90°，∠A=30°，AB=2．按以下步骤作图：
①分别以点A和点B为圆心，以大于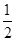
AB的长为半径画弧，两弧相交于点M、N；
②作直线MN，交AC于点D；
③连接BD．
则△BCD的周长为 ．
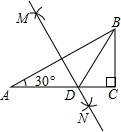
①分别以点A和点B为圆心，以大于
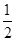AB的长为半径画弧，两弧相交于点M、N；②作直线MN，交AC于点D；
③连接BD．
则△BCD的周长为 ．
先根据锐角三角函数的定义求出BC及AC的长，再得出MN是线段AB的垂直平分线，由线段垂直平分线的性质即可得出结论．
解：∵在△ABC中，∠C=90°，∠A=30°，AB=2，
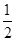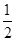∴BC=AB=×2=1，AC=AB•cos30°=2×
= 
，
∵分别以点A和点B为圆心，以大于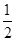AB的长为半径画弧，两弧相交于点M、N，
∴直线MN是线段AB的垂直平分线，
∴AD=BD，
∴△BCD的周长=（AD+CD）+BC=AC+BC=．
解：∵在△ABC中，∠C=90°，∠A=30°，AB=2，
∴BC=
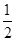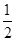AB=×2=1，AC=AB•cos30°=2×= ，∵分别以点A和点B为圆心，以大于
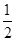AB的长为半径画弧，两弧相交于点M、N，∴直线MN是线段AB的垂直平分线，
∴AD=BD，
∴△BCD的周长=（AD+CD）+BC=AC+BC=
．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
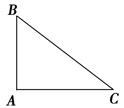
，∠ACB = 45°．
，如果将△ABC沿直线l翻折后，点B落在边AC的中点处，直线l与边BC交于点D，那么BD的长为 ．
