题目内容
在△ABC中,CA=CB,在△AED中, DA=DE,点D、E分别在CA、AB上.
(1)如图①,若∠ACB=∠ADE=90°,则CD与BE的数量关系是 ;
(2)若∠ACB=∠ADE=120°,将△AED绕点A旋转至如图②所示的位置,则CD与BE的数量关系是 ;,
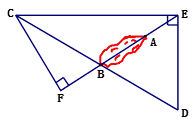
(3)若∠ACB=∠ADE=2α(0°< α < 90°),将△AED绕点A旋转至如图③所示的位置,探究线段CD与BE的数量关系,并加以证明(用含α的式子表示).

(1)如图①,若∠ACB=∠ADE=90°,则CD与BE的数量关系是 ;
(2)若∠ACB=∠ADE=120°,将△AED绕点A旋转至如图②所示的位置,则CD与BE的数量关系是 ;,
(3)若∠ACB=∠ADE=2α(0°< α < 90°),将△AED绕点A旋转至如图③所示的位置,探究线段CD与BE的数量关系,并加以证明(用含α的式子表示).

(1)BE=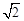 CD;(2)BE=
CD;(2)BE= CD;(3)BE=2CD·sinα,证明见解析.
CD;(3)BE=2CD·sinα,证明见解析.
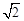 CD;(2)BE=
CD;(2)BE= CD;(3)BE=2CD·sinα,证明见解析.
CD;(3)BE=2CD·sinα,证明见解析.试题分析:(1)由已知,△ADE和△ACB都是等腰直角三角形,所以有AE=
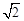 AD,AB=
AD,AB=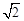 AC,从而有
AC,从而有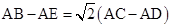 ,即BE=
,即BE=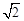 CD.
CD.(2)如图,分别过点C、D作CM⊥AB于点M,DN⊥AE于点N,
∵CA=CB,DA=DE,∠ACB=∠ADE=120°,
∴∠CAB=∠DAE,∠ACM=∠ADN="60°" ,AM=
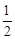 AB,AN=
AB,AN=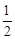 AE.
AE.∴∠CAD=∠BAE.
在Rt△ACM和Rt△ADN中,sin∠ACM=
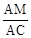 =
=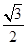 ,sin∠ADN=
,sin∠ADN=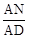 =
=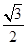 ,
,∴
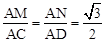 .∴
.∴ .
.又∵∠CAD=∠BAE,∴△BAE∽△CAD.∴
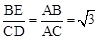 .∴BE=
.∴BE= CD.
CD.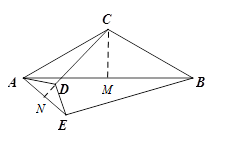
(3)根据等腰三角形的性质和锐角三角函数定义求得
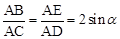 ,再由△BAE∽△CAD得出
,再由△BAE∽△CAD得出 ,从而得出结论.
,从而得出结论.(1)BE=
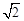 CD.
CD.(2)BE=
 CD.
CD.(3)BE=2CD·sinα.证明如下:
如图,分别过点C、D作CM⊥AB于点M,DN⊥AE于点N,
∵CA=CB,DA=DE,∠ACB=∠ADE="2α" ,
∴∠CAB=∠DAE,∠ACM=∠ADN="α" ,AM=
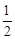 AB,AN=
AB,AN=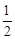 AE.
AE.∴∠CAD=∠BAE.
在Rt△ACM和Rt△ADN中,sin∠ACM=
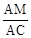 ,sin∠ADN=
,sin∠ADN=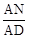 ,
,∴
 .∴
.∴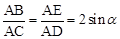 .
.又∵∠CAD=∠BAE,∴△BAE∽△CAD.∴
 .
.∴BE=2DC·sinα.


练习册系列答案
相关题目

 的值为 .
的值为 . .
.
 cm, E为CD边上的中点,点P从点A沿折线AE-EC运动到点C时停止,点Q从点A沿折线AB-BC运动到点C时停止,它们运动的速度都是1cm/s.如果点P,Q同时开始运动,设运动时间为t(s),△APQ的面积为
cm, E为CD边上的中点,点P从点A沿折线AE-EC运动到点C时停止,点Q从点A沿折线AB-BC运动到点C时停止,它们运动的速度都是1cm/s.如果点P,Q同时开始运动,设运动时间为t(s),△APQ的面积为 ,则y与t的函数关系的图象可能是( )
,则y与t的函数关系的图象可能是( )




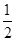 AB的长为半径画弧,两弧相交于点M、N;
AB的长为半径画弧,两弧相交于点M、N;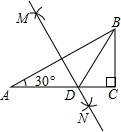
 小时到达B处,那么tan∠ABP=( )
小时到达B处,那么tan∠ABP=( )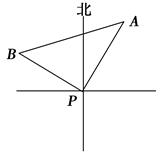
 cm
cm cm
cm cm
cm cm
cm