题目内容
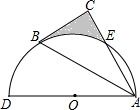（2013•襄阳）如图，以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点，交直角边AC于点E，B、E是半圆弧的三等分点，弧BE的长为| 2 |
| 3 |
分析：首先根据圆周角定理得出扇形半径以及圆周角度数，进而利用锐角三角函数关系得出BC，AC的长，利用S△ABC-S扇形BOE=图中阴影部分的面积求出即可．
解答：
解：连接BD，BE，BO，EO，
∵B，E是半圆弧的三等分点，
∴∠EOA=∠EOB=∠BOD=60°，
∴∠BAC=30°，
∵弧BE的长为
π，
∴
=
π，
解得：R=2，
∴AB=ADcos30°=2
，
∴BC=
AB=
，
∴AC=
=3，
∴S△ABC=
×BC×AC=
×
×3=
，
∵△BOE和△ABE同底等高，
∴△BOE和△ABE面积相等，
∴图中阴影部分的面积为：S△ABC-S扇形BOE=
-
=
-
．
故选：D．
解：连接BD，BE，BO，EO，∵B，E是半圆弧的三等分点，
∴∠EOA=∠EOB=∠BOD=60°，
∴∠BAC=30°，
∵弧BE的长为
| 2 |
| 3 |
∴
| 60π×R |
| 180 |
| 2 |
| 3 |
解得：R=2，
∴AB=ADcos30°=2
| 3 |
∴BC=
| 1 |
| 2 |
| 3 |
∴AC=
| AB2-BC2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
3
| ||
| 2 |
∵△BOE和△ABE同底等高，
∴△BOE和△ABE面积相等，
∴图中阴影部分的面积为：S△ABC-S扇形BOE=
3
| ||
| 2 |
| 60π×22 |
| 360 |
3
| ||
| 2 |
| 2π |
| 3 |
故选：D．
点评：此题主要考查了扇形的面积计算以及三角形面积求法等知识，根据已知得出∴△BOE和△ABE面积相等是解题关键．
练习册系列答案
相关题目
（2013•襄阳）如图，BD平分∠ABC，CD∥AB，若∠BCD=70°，则∠ABD的度数为（ ）
（2013•襄阳）如图，平行四边形ABCD的对角线交于点O，且AB=5，△OCD的周长为23，则平行四边形ABCD的两条对角线的和是（ ）
（2013•襄阳）如图，水平放置的圆柱形排水管道的截面直径是1m，其中水面的宽AB为0.8m，则排水管内水的深度为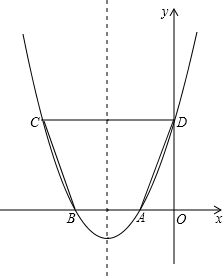
（2013•襄阳）如图，已知抛物线y=ax2+bx+c与x轴的一个交点A的坐标为（-1，0），对称轴为直线x=-2．