题目内容
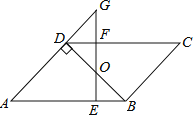
【题目】如图，矩形纸片
中，
，把纸片沿直线
折叠，点
落在
处，
交
于点
，若
，则
的面积为（ ）
A.
B.
C.
D.
【答案】A
【解析】
由矩形的性质可得∠B=90°，AB∥CD，可得∠DCA=∠CAB，由折叠的性质可得BC=EC=4cm，AB=AE，∠E=∠B=90°，∠EAC=∠CAB=∠DCA，可得AO=OC=5cm，由勾股定理可求OE的长，即可求△ABC的面积．
解：∵四边形ABCD是矩形
∴∠B=90°，AB∥CD
∴∠DCA=∠CAB
∵把纸片ABCD沿直线AC折叠，点B落在E处，
∴BC=EC=4cm，AB=AE，∠E=∠B=90°，∠EAC=∠CAB，
∴∠DCA=∠EAC
∴AO=OC=5cm
∴
，
∴AE=AO+OE=8cm，
∴AB=8cm，
∴△ABC的面积=
×AB×BC=16cm2，
故选：A．
练习册系列答案
相关题目
