Question

【题目】如图，在圆心角为135°的扇形OAB中，半径OA=2cm，点C，D为 的三等分点，连接OC，OD，AC，CD，BD，则图中阴影部分的面积为cm2 ．

Answer 1

【答案】 π﹣3
【解析】解：如图作DH⊥OB于H．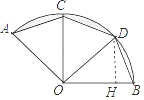

∵点C，D为 的三等分点，∠AOB=135°，
∴∠AOC=∠COD=∠DOB=45°，
∴△ODH是等腰直角三角形，△AOC≌△COD≌△DOB，
∵OD=2，
∴DH=OH= ，
∴S△ODB= OBDH= ，
∴S△AOC=S△COD=S△DOB= ，
∴S阴= ﹣3S△DOB=（ π﹣3 ）cm2 ，
故答案为（ π﹣3 ）cm2 ．
根据题意可作辅助线，过点D作DH⊥OB于H，由点C，D为 弧 A B 的三等分点可得△AOC≌△COD≌△DOB，所以S阴 =扇形AOB的面积-3S△DOB， 而扇形AOB的面积=n360,在三角形DOB中根据已知条件可求高DH，代入上式计算即可求解。