题目内容
 如图,△ABC中,∠C=90°,AC=8cm,AB=10cm,点P由点C出发以每秒2 cm的速度沿线CA向点A运动(不运动至A点),⊙O的圆心在BP上,且⊙O分别与AB、AC相切,当点P运动2秒钟时,⊙O的半径是
如图,△ABC中,∠C=90°,AC=8cm,AB=10cm,点P由点C出发以每秒2 cm的速度沿线CA向点A运动(不运动至A点),⊙O的圆心在BP上,且⊙O分别与AB、AC相切,当点P运动2秒钟时,⊙O的半径是
- A.
 cm
cm - B.
 cm
cm - C.
 cm
cm - D.2cm
A
分析:本题较复杂,设AC、AB与⊙O的切点分别为R、M,连接OR、OM,过O作OK⊥BC于K;由于△POR∽△PCB,可得出关于PR,OR,PC,BC的比例关系式,由此可求出PR与半径的比例关系.由此可表示出OK,AP的长;在Rt△OBK中,已知了OK的表达式,BK=BC-r,而OB可在Rt△OBM中用勾股定理求得.由此可根据勾股定理求出半径r的长.
解答: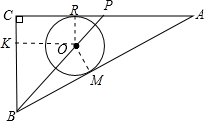 解:连接OR、OM,
解:连接OR、OM,
则OR⊥AC,OM⊥AB;过O作OK⊥BC于K,
设⊙O的半径为r,
易知:△POR∽△PBC,
∴ ,
,
∵BC=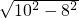 =6cm,
=6cm,
∴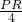 =
=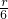 ,即:PR=
,即:PR=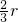 ,
,
AP=CP=2×2=4cm,
在Rt△BOK与Rt△BMO中,根据勾股定理,得:
(6-r)2+(4- r)2=BO2=[10-(8-4+
r)2=BO2=[10-(8-4+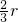 )]2+r2
)]2+r2
解得:r= cm.
cm.
故本题选A.
点评:此题虽是动点问题,但和动点无直接关系,实质是运用切线的性质和勾股定理得到一个关于半径的方程,然后求解.
分析:本题较复杂,设AC、AB与⊙O的切点分别为R、M,连接OR、OM,过O作OK⊥BC于K;由于△POR∽△PCB,可得出关于PR,OR,PC,BC的比例关系式,由此可求出PR与半径的比例关系.由此可表示出OK,AP的长;在Rt△OBK中,已知了OK的表达式,BK=BC-r,而OB可在Rt△OBM中用勾股定理求得.由此可根据勾股定理求出半径r的长.
解答:
 解:连接OR、OM,
解:连接OR、OM,则OR⊥AC,OM⊥AB;过O作OK⊥BC于K,
设⊙O的半径为r,
易知:△POR∽△PBC,
∴
 ,
,∵BC=
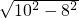 =6cm,
=6cm,∴
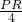 =
=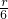 ,即:PR=
,即:PR=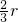 ,
,AP=CP=2×2=4cm,
在Rt△BOK与Rt△BMO中,根据勾股定理,得:
(6-r)2+(4-
 r)2=BO2=[10-(8-4+
r)2=BO2=[10-(8-4+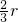 )]2+r2
)]2+r2解得:r=
 cm.
cm.故本题选A.
点评:此题虽是动点问题,但和动点无直接关系,实质是运用切线的性质和勾股定理得到一个关于半径的方程,然后求解.

练习册系列答案
相关题目
 26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB.
26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB. 27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE.
27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE. 27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M
27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M 14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( )
14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( ) 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.