Question

已知直线l与⊙O，AB是⊙O的直径，AD⊥l于点D．

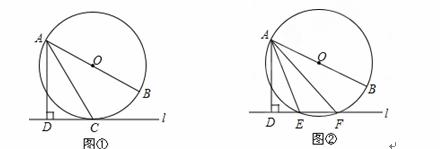
   （1）如图①，当直线l与⊙O相切于点C时，若∠DAC=30°，求∠BAC的大小；

（2）如图②，当直线l与⊙O相交于点E、F时，若∠DAE=18°，求∠BAF的大小．

Answer 1

解：（1）如图①，连接OC，

∵直线l与⊙O相切于点C，∴OC⊥l，

∵AD⊥l，∴OC∥AD，∴∠OCA=∠DAC，

∵OA=OC，∴∠BAC=∠OCA，

∴∠BAC=∠DAC=30°；                    ………………（6分）

（2）如图②，连接BF，

∵AB是⊙O的直径，∴∠AFB=90°，∴∠BAF=90°-∠B，

∴∠AEF=∠ADE+∠DAE=90°+18°=108° ………………（8分）

在⊙O中，四边形ABFE是圆的内接四边形，

∴∠AEF+∠B=180°       ∴∠B=180°-108°=72°

∴∠BAF=90°-∠B=90°-72°=18°．       ………………（12分）