题目内容
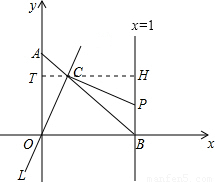
 (2008•房山区一模)如图,点A在y轴上,点B在x轴上,且OA=OB=1,经过原点O的直线l交线段AB于点C,过C作OC的垂线,与直线x=1相交于点P,现将直线L绕O点旋转,使交点C从A向B运动,但C点必须在第一象限内,并记AC的长为t,分析此图后,对下列问题作出探究:
(2008•房山区一模)如图,点A在y轴上,点B在x轴上,且OA=OB=1,经过原点O的直线l交线段AB于点C,过C作OC的垂线,与直线x=1相交于点P,现将直线L绕O点旋转,使交点C从A向B运动,但C点必须在第一象限内,并记AC的长为t,分析此图后,对下列问题作出探究:(1)当△AOC和△BCP全等时,求出t的值;
(2)通过动手测量线段OC和CP的长来判断它们之间的大小关系并证明你得到的结论;
(3)①设点P的坐标为(1,b),试写出b关于t的函数关系式和变量t的取值范围.
②求出当△PBC为等腰三角形时点P的坐标.
【答案】分析:(1)△AOC和△BCP全等,则AO=BC=1,又∵AB=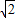 ,t=AB-BC=
,t=AB-BC=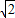 -1;
-1;
(2)过点C作x轴的平行线,交OA与直线BP于点T、H,证△OTC≌△CHP即可;
(3)根据题意可直接得出b=1-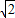 t;当t=0或1时,△PBC为等腰三角形,即P(1,1),P(1,1-
t;当t=0或1时,△PBC为等腰三角形,即P(1,1),P(1,1-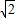 ),但t=0时,点C不在第一象限,所以不符合题意.
),但t=0时,点C不在第一象限,所以不符合题意.
解答:解:(1)△AOC和△BCP全等,则AO=BC=1,
又AB=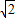 ,
,
所以t=AB-BC=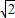 -1;
-1;
 (2)OC=CP.
(2)OC=CP.
证明:过点C作x轴的平行线,交OA与直线BP于点T、H.
∵PC⊥OC,
∴∠OCP=90°,
∵OA=OB=1,
∴∠OBA=45°,
∵TH∥OB,
∴∠BCH=45°,又∠CHB=90°,
∴△CHB为等腰直角三角形,
∴CH=BH,
∵∠AOB=∠OBH=∠BHT=90°,
∴四边形OBHT为矩形,∴OT=BH,
∴OT=CH,
∵∠TCO+∠PCH=90°,
∠CPH+∠PCH=90°,
∴∠TCO=∠CPH,
∵HB⊥x轴,TH∥OB,
∴∠CTO=∠THB=90°,TO=HC,∠TCO=∠CPH,
∴△OTC≌△CHP,
∴OC=CP;
(3)①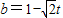 ;(0<t<
;(0<t<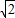 )
)
②t=0时,△PBC是等腰直角三角形,但点C与点A重合,不在第一象限,所以不符合,
PB=BC,则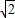 -t=|1-
-t=|1-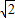 t|,
t|,
解得t=1或t=-1(舍去),
∴当t=1时,△PBC为等腰三角形,
即P点坐标为:P(1,1-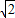 ).
).
点评:主要考查了函数和几何图形的综合运用.解题的关键是会灵活的运用函数的性质和点的意义表示出相应的线段的长度,再结合三角形全等和等腰三角形的性质求解.试题中贯穿了方程思想和数形结合的思想,请注意体会.
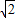 ,t=AB-BC=
,t=AB-BC=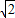 -1;
-1;(2)过点C作x轴的平行线,交OA与直线BP于点T、H,证△OTC≌△CHP即可;
(3)根据题意可直接得出b=1-
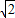 t;当t=0或1时,△PBC为等腰三角形,即P(1,1),P(1,1-
t;当t=0或1时,△PBC为等腰三角形,即P(1,1),P(1,1-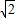 ),但t=0时,点C不在第一象限,所以不符合题意.
),但t=0时,点C不在第一象限,所以不符合题意.解答:解:(1)△AOC和△BCP全等,则AO=BC=1,
又AB=
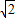 ,
,所以t=AB-BC=
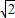 -1;
-1; (2)OC=CP.
(2)OC=CP.证明:过点C作x轴的平行线,交OA与直线BP于点T、H.
∵PC⊥OC,
∴∠OCP=90°,
∵OA=OB=1,
∴∠OBA=45°,
∵TH∥OB,
∴∠BCH=45°,又∠CHB=90°,
∴△CHB为等腰直角三角形,
∴CH=BH,
∵∠AOB=∠OBH=∠BHT=90°,
∴四边形OBHT为矩形,∴OT=BH,
∴OT=CH,
∵∠TCO+∠PCH=90°,
∠CPH+∠PCH=90°,
∴∠TCO=∠CPH,
∵HB⊥x轴,TH∥OB,
∴∠CTO=∠THB=90°,TO=HC,∠TCO=∠CPH,
∴△OTC≌△CHP,
∴OC=CP;
(3)①
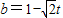 ;(0<t<
;(0<t<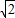 )
)②t=0时,△PBC是等腰直角三角形,但点C与点A重合,不在第一象限,所以不符合,
PB=BC,则
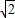 -t=|1-
-t=|1-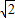 t|,
t|,解得t=1或t=-1(舍去),
∴当t=1时,△PBC为等腰三角形,
即P点坐标为:P(1,1-
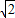 ).
).点评:主要考查了函数和几何图形的综合运用.解题的关键是会灵活的运用函数的性质和点的意义表示出相应的线段的长度,再结合三角形全等和等腰三角形的性质求解.试题中贯穿了方程思想和数形结合的思想,请注意体会.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
(2008•房山区一模)为响应国家要求中小学生每天锻练1小时的号召,某校准备开展“阳光体育运动”的活动.校学生会围绕着“你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行了随机抽样调查,从而得到一组数据.绘制如下的统计图表:
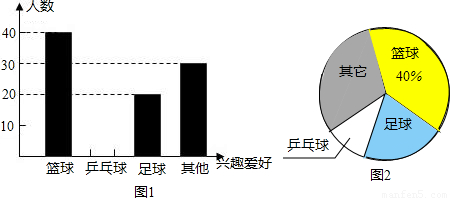
各年级学生人数统计表
(1)该校对多少名学生进行了抽样调查?
(2)请在图1中将“乒乓球”部分的图形补充完整;若该校九年级学生比八年级学生多40人,请你计算该校九年级有学生多少人?(填写表格中缺失的数据)
(3)请你估计全校学生中最喜欢足球活动的人数约为多少人?

各年级学生人数统计表
| 七年级 | 八年级 | 九年级 | |
| 学生人数 | 240 | 360 |
(2)请在图1中将“乒乓球”部分的图形补充完整;若该校九年级学生比八年级学生多40人,请你计算该校九年级有学生多少人?(填写表格中缺失的数据)
(3)请你估计全校学生中最喜欢足球活动的人数约为多少人?
(2008•房山区一模)为响应国家要求中小学生每天锻练1小时的号召,某校准备开展“阳光体育运动”的活动.校学生会围绕着“你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行了随机抽样调查,从而得到一组数据.绘制如下的统计图表:
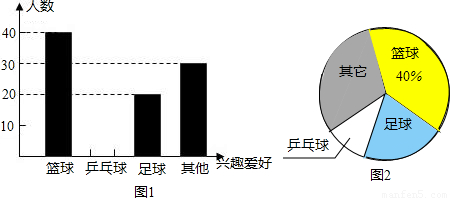
各年级学生人数统计表
(1)该校对多少名学生进行了抽样调查?
(2)请在图1中将“乒乓球”部分的图形补充完整;若该校九年级学生比八年级学生多40人,请你计算该校九年级有学生多少人?(填写表格中缺失的数据)
(3)请你估计全校学生中最喜欢足球活动的人数约为多少人?

各年级学生人数统计表
| 七年级 | 八年级 | 九年级 | |
| 学生人数 | 240 | 360 |
(2)请在图1中将“乒乓球”部分的图形补充完整;若该校九年级学生比八年级学生多40人,请你计算该校九年级有学生多少人?(填写表格中缺失的数据)
(3)请你估计全校学生中最喜欢足球活动的人数约为多少人?