题目内容
点D是⊙O的直径CA延长线上一点,点B在⊙O上,∠DBA=∠C.【小题1】请判断BD所在的直线与⊙O的位置关系,并说明理由;
【小题2】若AD=AO=1,求图中阴影部分的面积(结果保留根号).

【小题1】BD所在的直线与⊙O相切.
理由如下:
连接OB. ∵CA是⊙O的直径,∴∠ABC=90°.
∵OB="OC," ∴∠OBC="∠C."
∵∠DBA=∠C, ∴∠DBA+∠OBA=∠OBC+∠OBA=∠ABC=90°.
∴OB⊥BD.
∵点B在⊙O上, ∴ BD所在的直线与⊙O相切.
【小题1】∵∠DBO="90°," OB=AD.∴AB="OA=OB=1." ∴∆ABC是等边三角形, ∠AOB=60°.
∵S扇=
 , S∆ABC=
, S∆ABC= ,
,∴S阴= S∆ABC-S扇=
 . 解析:
. 解析:【小题1】由OB⊥BD可以得出BD所在的直线与⊙O相切。
【小题1】分别算出扇形面积和三角形面积,两者相减即可得出阴影部分的面积。

练习册系列答案
相关题目
 已知:如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且OA=AB=AD.
已知:如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且OA=AB=AD.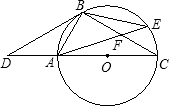 本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分.
本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分. 点D是⊙O的直径CA延长线上一点,点B在⊙O上,BD是⊙O的切线,且AB=AD.
点D是⊙O的直径CA延长线上一点,点B在⊙O上,BD是⊙O的切线,且AB=AD.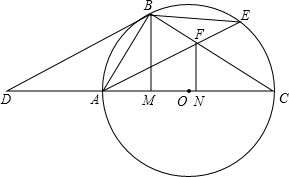 =30°.
=30°.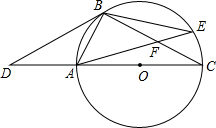 如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且AB=AD=AO.
如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且AB=AD=AO.