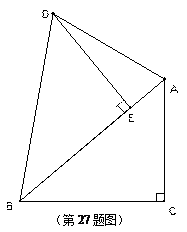
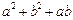题目内容
如图9,边长为5的正方形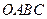 的顶点
的顶点 在坐标原点处,点
在坐标原点处,点 分别在
分别在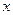 轴、
轴、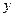 轴的正半轴上,点
轴的正半轴上,点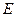 是
是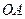 边上的点(不与点
边上的点(不与点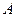 重合),
重合), ,且与正方形外角平分线
,且与正方形外角平分线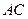 交于点
交于点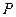 .
.
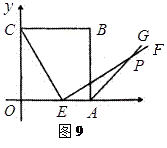
(1)当点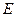 坐标为
坐标为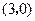 时,试证明
时,试证明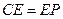 ;
;
(2)如果将上述条件“点 坐标为(3,0)”改为“点
坐标为(3,0)”改为“点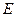 坐标为(
坐标为(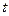 ,0)(
,0)(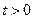 )”,结论
)”,结论
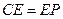 是否仍然成立,请说明理由;
是否仍然成立,请说明理由;
(3)在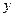 轴上是否存在点
轴上是否存在点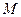 ,使得四边形
,使得四边形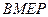 是平行四边形?若存在,用
是平行四边形?若存在,用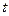 表示点
表示点
的坐标;若不存在,说明理由.
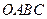 的顶点
的顶点 在坐标原点处,点
在坐标原点处,点 分别在
分别在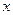 轴、
轴、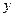 轴的正半轴上,点
轴的正半轴上,点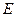 是
是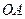 边上的点(不与点
边上的点(不与点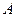 重合),
重合), ,且与正方形外角平分线
,且与正方形外角平分线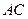 交于点
交于点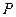 .
.
(1)当点
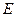 坐标为
坐标为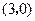 时,试证明
时,试证明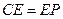 ;
;(2)如果将上述条件“点
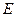 坐标为(3,0)”改为“点
坐标为(3,0)”改为“点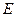 坐标为(
坐标为(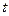 ,0)(
,0)(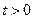 )”,结论
)”,结论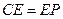 是否仍然成立,请说明理由;
是否仍然成立,请说明理由;(3)在
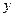 轴上是否存在点
轴上是否存在点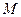 ,使得四边形
,使得四边形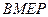 是平行四边形?若存在,用
是平行四边形?若存在,用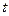 表示点
表示点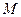
的坐标;若不存在,说明理由.
(1)略
(2)成立,证明略
(3)点
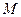 的坐标为
的坐标为
解:(1)过点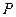 作
作 轴,垂足为
轴,垂足为

∴ ∵
∵ ∴
∴
∴ ∴
∴ 2′
2′
由题意知:


∴ 得
得
∴ 3′
3′
在 和
和 中
中
∴

故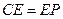 5′
5′
(2)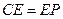 仍成立.
仍成立.
同理 ∴
∴ 6′
6′
由题意知:


∴ 整理得
整理得
∵点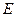 不与点
不与点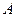 重合 ∴
重合 ∴ ∴
∴

∴在 和
和 中
中

 ∴
∴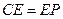 5′
5′
(3)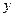 轴上存在点
轴上存在点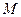 ,使得四边形
,使得四边形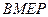 是平行四边形. 9′
是平行四边形. 9′
过点 作
作 交
交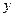 轴于点
轴于点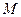
∴ ∴
∴
在 和
和 中
中
 ∴
∴ ∴
∴
而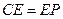 ∴
∴
由于 ∴四边形
∴四边形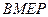 是平行四边形. 11′
是平行四边形. 11′
故 可得
可得 ∴
∴
故点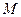 的坐标为
的坐标为 12′[
12′[
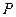 作
作 轴,垂足为
轴,垂足为

∴
 ∵
∵ ∴
∴
∴
 ∴
∴ 2′
2′由题意知:



∴
 得
得
∴
 3′
3′在
 和
和 中
中∴


故
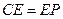 5′
5′(2)
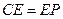 仍成立.
仍成立.同理
 ∴
∴ 6′
6′由题意知:



∴
 整理得
整理得
∵点
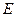 不与点
不与点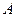 重合 ∴
重合 ∴ ∴
∴

∴在
 和
和 中
中
 ∴
∴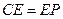 5′
5′(3)
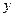 轴上存在点
轴上存在点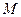 ,使得四边形
,使得四边形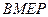 是平行四边形. 9′
是平行四边形. 9′过点
 作
作 交
交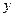 轴于点
轴于点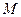
∴
 ∴
∴
在
 和
和 中
中 ∴
∴ ∴
∴
而
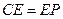 ∴
∴
由于
 ∴四边形
∴四边形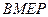 是平行四边形. 11′
是平行四边形. 11′故
 可得
可得 ∴
∴
故点
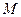 的坐标为
的坐标为 12′[
12′[
练习册系列答案
相关题目
 的对角线
的对角线 和
和 相交于点
相交于点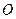 ,
,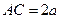 ,
,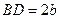 ,
,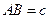
 ,
, ,求
,求 中,
中,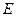 是
是 边上一点,
边上一点, 为
为 延长线上的点,
延长线上的点, .
.
 ≌△
≌△
 ,求
,求 的度数
的度数
 ,且AD=10,求AB的长(7分)
,且AD=10,求AB的长(7分) ,使衣帽架拉伸或收缩.当菱形的边长为
,使衣帽架拉伸或收缩.当菱形的边长为 时,
时, 两点的距离为_______cm.
两点的距离为_______cm.

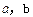 的矩形,它的周长为14,面积为10,求下列各式的值:(1)
的矩形,它的周长为14,面积为10,求下列各式的值:(1)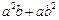 (2)
(2)