ЬтФПФкШн
ЁОЬтФПЁПШчЭМ1ЃЌЫФБпаЮ![]() ЪЧе§ЗНаЮЃЌЖЏЕу
ЪЧе§ЗНаЮЃЌЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌвд
ГіЗЂЃЌвд![]() cm/sЕФЫйЖШбиБп
cm/sЕФЫйЖШбиБп![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() дШЫйдЫЖЏЕН
дШЫйдЫЖЏЕН![]() жежЙЃЛЖЏЕу
жежЙЃЛЖЏЕу![]() Дг
Дг![]() ГіЗЂЃЌвд
ГіЗЂЃЌвд![]() cm/sЕФЫйЖШбиБп
cm/sЕФЫйЖШбиБп![]() дШЫйдЫЖЏЕН
дШЫйдЫЖЏЕН![]() жежЙЃЌШє
жежЙЃЌШє![]() ЁЂ
ЁЂ![]() СНЕуЭЌЪБГіЗЂЃЌдЫЖЏЪБМфЮЊ
СНЕуЭЌЪБГіЗЂЃЌдЫЖЏЪБМфЮЊ![]() sЃЌЁї
sЃЌЁї![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() cm2.
cm2. ![]() гы
гы![]() жЎМфКЏЪ§ЙиЯЕЕФЭМЯёШчЭМ
жЎМфКЏЪ§ЙиЯЕЕФЭМЯёШчЭМ![]() ЫљЪО.
ЫљЪО.
ЃЈ1ЃЉЧѓЭМ![]() жаЯпЖЮ
жаЯпЖЮ![]() ЫљБэЪОЕФКЏЪ§ЙиЯЕЪНЃЛ
ЫљБэЪОЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЕБЖЏЕу![]() дкБп
дкБп![]() дЫЖЏЕФЙ§ГЬжаЃЌШєвд
дЫЖЏЕФЙ§ГЬжаЃЌШєвд![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃЌЧѓ
ЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉЪЧЗёДцдкетбљЕФ![]() ЃЌЪЙ
ЃЌЪЙ![]() НЋе§ЗНаЮ
НЋе§ЗНаЮ![]() ЕФУцЛ§ЧЁКУЗжГЩ
ЕФУцЛ§ЧЁКУЗжГЩ![]() ЕФСНВПЗжЃПШєДцдкЃЌЧѓГіетбљЕФ
ЕФСНВПЗжЃПШєДцдкЃЌЧѓГіетбљЕФ![]() ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЖЮЕФКЏЪ§БэДяЪНЮЊ
ЖЮЕФКЏЪ§БэДяЪНЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБ![]() Лђ
Лђ![]() ЪБЃЌвд
ЪБЃЌвд![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃЛ
ЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃЛ
ЃЈ3ЃЉДцдк![]() КЭ
КЭ![]() ЃЌЪЙ
ЃЌЪЙ![]() НЋе§ЗНаЮ
НЋе§ЗНаЮ![]() ЕФУцЛ§ЧЁКУЗжГЩ
ЕФУцЛ§ЧЁКУЗжГЩ![]() ЕФСНВПЗжЃЎ
ЕФСНВПЗжЃЎ
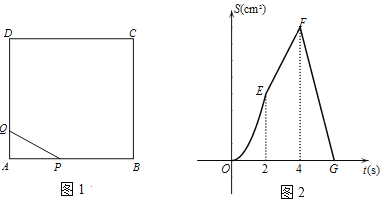
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉКЏЪ§ЭМЯѓжаЯпЖЮFGЃЌБэЪОЕуQдЫЖЏжСжеЕуDжЎКѓЭЃжЙдЫЖЏЃЌЖјЕуPдкЯпЖЮCDЩЯМЬајдЫЖЏЕФЧщаЮЃЎШчЭМ2ЫљЪОЃЌЧѓГіSЕФБэДяЪНЃЌВЂШЗЖЈtЕФШЁжЕЗЖЮЇЃЛЃЈ2ЃЉЗжРрЬжТлЃЌСаЗНГЬЧѓНтМДПЩЃЛ
ЃЈ3ЃЉЕБЕуPдкABЩЯдЫЖЏЪБЃЌPQНЋе§ЗНаЮABCDЗжГЩЁїAPQКЭЮхБпаЮPBCDQСНВПЗжЃЌШчЭМ3ЫљЪОЃЌЧѓГіtЕФжЕЃЛЕБЕуPдкBCЩЯдЫЖЏЪБЃЌPQНЋСтаЮЗжЮЊЬнаЮABPQКЭЬнаЮPCDQСНВПЗжЃЌШчЭМ4ЫљЪОЃЌЧѓГіtЕФжЕЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉгЩЬтвтЃЌПЩжЊЬтЭМ2жаЕу![]() БэЪОЕу
БэЪОЕу![]() дЫЖЏжСЕу
дЫЖЏжСЕу![]() ЪБЕФЧщаЮЃЌЫљгУЪБМфЮЊ
ЪБЕФЧщаЮЃЌЫљгУЪБМфЮЊ![]() sЃЌдђе§ЗНаЮЕФБпГЄ
sЃЌдђе§ЗНаЮЕФБпГЄ![]() cmЃЎЕу
cmЃЎЕу![]() дЫЖЏжСЕу
дЫЖЏжСЕу![]() ЫљашЪБМфЮЊЃК
ЫљашЪБМфЮЊЃК ![]() sЃЌЕу
sЃЌЕу![]() дЫЖЏжСжеЕу
дЫЖЏжСжеЕу![]() ЫљашЪБМфЮЊ
ЫљашЪБМфЮЊ![]() sЃЎ
sЃЎ
вђДЫдк![]() ЖЮФкЃЌЕу
ЖЮФкЃЌЕу![]() дЫЖЏжСЕу
дЫЖЏжСЕу![]() ЭЃжЙдЫЖЏЃЌЕу
ЭЃжЙдЫЖЏЃЌЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯМЬајдЫЖЏЃЌЧвЪБМф
ЩЯМЬајдЫЖЏЃЌЧвЪБМф![]() ЕФШЁжЕЗЖЮЇЮЊ
ЕФШЁжЕЗЖЮЇЮЊ![]() ЃЎ
ЃЎ
ЙЪ![]() ЃЌ
ЃЌ
Ёр![]() ЖЮЕФКЏЪ§БэДяЪНЮЊ
ЖЮЕФКЏЪ§БэДяЪНЮЊ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЂйШє![]() ЃЌдђ
ЃЌдђ![]() ЃЌЯдШЛВЛГЩСЂ
ЃЌЯдШЛВЛГЩСЂ
ЂкШє![]() ЃЌдђ
ЃЌдђ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ ![]() ЃЈЩсШЅЃЉ
ЃЈЩсШЅЃЉ
ЂлШє![]() ЃЌдђ
ЃЌдђ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ ![]() ЃЈЩсШЅЃЉ
ЃЈЩсШЅЃЉ
злЩЯЫљЪіЃЌЕБ![]() Лђ
Лђ![]() ЪБЃЌвд
ЪБЃЌвд![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮ
ЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮ
ЃЈ3ЃЉМйЩшДцдкетбљЕФ![]() ЃЌЪЙ
ЃЌЪЙ![]() НЋе§ЗНаЮ
НЋе§ЗНаЮ![]() ЕФУцЛ§ЧЁКУЗжГЩ
ЕФУцЛ§ЧЁКУЗжГЩ![]() ЕФСНВПЗж.взЕУе§ЗНаЮ
ЕФСНВПЗж.взЕУе§ЗНаЮ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЎ
ЃЎ
ЂйЕБЕу![]() дк
дк![]() ЩЯдЫЖЏЪБЃЌ
ЩЯдЫЖЏЪБЃЌ ![]() НЋе§ЗНаЮ
НЋе§ЗНаЮ![]() ЗжГЩЁї
ЗжГЩЁї![]() КЭЮхБпаЮ
КЭЮхБпаЮ![]() СНВПЗжЃЌШчЭМЫљЪОЃЌИљОнЬтвтЃЌЕУ
СНВПЗжЃЌШчЭМЫљЪОЃЌИљОнЬтвтЃЌЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЛ
ЃЛ
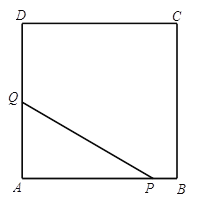
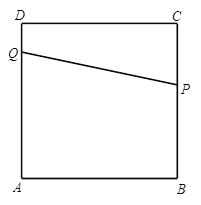
ЭМ3 ЭМ4
ЂкЕБЕу![]() дк
дк![]() ЩЯдЫЖЏЪБЃЌ
ЩЯдЫЖЏЪБЃЌ ![]() НЋе§ЗНаЮ
НЋе§ЗНаЮ![]() ЗжЮЊЬнаЮ
ЗжЮЊЬнаЮ![]() КЭЬнаЮ
КЭЬнаЮ![]() СНВПЗжЃЌШчЭМЫљЪОЃЎИљОнЬтвтЃЌЕУ
СНВПЗжЃЌШчЭМЫљЪОЃЎИљОнЬтвтЃЌЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЎ
ЃЎ
ЁрДцдк![]() КЭ
КЭ![]() ЃЌЪЙ
ЃЌЪЙ![]() НЋе§ЗНаЮ
НЋе§ЗНаЮ![]() ЕФУцЛ§ЧЁКУЗжГЩ
ЕФУцЛ§ЧЁКУЗжГЩ![]() ЕФСНВПЗжЃЎ
ЕФСНВПЗжЃЎ

 аЧМЖПкЫуЬьЬьСЗЯЕСаД№АИ
аЧМЖПкЫуЬьЬьСЗЯЕСаД№АИ УЂЙћНЬИЈДяБъВтЪдОэЯЕСаД№АИ
УЂЙћНЬИЈДяБъВтЪдОэЯЕСаД№АИЁОЬтФПЁПАЫЃЈ2ЃЉАрзщжЏСЫвЛДЮОЕфРЪЖСБШШќЃЌМзЁЂввСНЖгИї10ШЫЕФБШШќГЩМЈШчБэЃЈ10ЗжжЦЃЉЃК
Мз | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
вв | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
ЃЈ1ЃЉМзЖгГЩМЈЕФжаЮЛЪ§ЪЧЗжЃЌввЖгГЩМЈЕФжкЪ§ЪЧЗжЃЛ
ЃЈ2ЃЉМЦЫуМзЁЂввЖгЕФЦНОљГЩМЈКЭЗНВюЃЌЪдЫЕУїГЩМЈНЯЮЊећЦыЕФЪЧФФвЛЖгЃП


