题目内容
【题目】如图,⊙M交x轴于A(﹣1,0),B(3,0)两点.交y轴于C(0,3),D(0,1)两点.
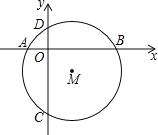
(1)求点M的坐标;
(2)求弧BD的长.
【答案】(1)M(1,﹣1);(2)![]() π.
π.
【解析】
试题分析:(1)过M点作ME⊥AB于E,MF⊥CD于F,连接MB,MC,由垂径定理得出EB=![]() AB=2,得出OE=1,同理可得OF=1,证四边形OEMF为正方形,得出EM=EF=1,即可得出结果;
AB=2,得出OE=1,同理可得OF=1,证四边形OEMF为正方形,得出EM=EF=1,即可得出结果;
(2)连接MD,BC,由勾股定理可得BM=![]() ,证出∠BCO=45°,得出∠BMD=90°,由弧长公式即可得出结果.
,证出∠BCO=45°,得出∠BMD=90°,由弧长公式即可得出结果.
解:(1)如图1所示,过M点作ME⊥AB于E,MF⊥CD于F,连接MB,MC,
则EB=![]() AB=2,四边形OENF是矩形,
AB=2,四边形OENF是矩形,
∴OE=1,
同理可得OF=1,
∴OEOF,
∴四边形OEMF为正方形,
∴EM=EF=1,
∴M(1,﹣1);
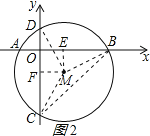
(2)连接MD,BC,如图2所示:
由勾股定理可得BM=![]() ,
,
∵∠BOC=90°,OB=OC,
∴∠BCO=45°,
∴∠BMD=90°,
∴弧BD的长=![]() =
=![]() π.
π.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目