Question

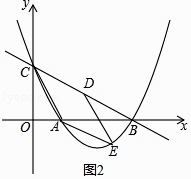
【题目】如图，抛物线y=a（x﹣1）（x﹣4）与x轴相交于点A、B（点A在点B的左侧），与x轴相交于点C，点D在线段CB上（点D不与B、C重合），过点D作CA的平行线，与抛物线相交于点E，直线BC的解析式为y=kx+2．

（1）抛物线的解析式为；
（2）求线段DE的最大值；
（3）当点D为BC的中点时，判断四边形CAED的形状，并加以证明．

Answer 1

【答案】
（1）y= x2﹣ x+2
（2）

解：如图1，过点D、E分别作y轴、x轴的平行线，两线相交于点F，

当y=0时， （x﹣1）（x﹣4）=0，解得x1=1，x2=4，则A（1，0），B（4，0），

设直线BC的解析式为y=kx+b，

把C（0，2），B（4，0）代入得 ，解得 ，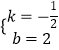

∴直线BC的解析式为y=﹣ x+2，

设E（m， m2﹣ m+2），EF=n，则D（m﹣n，﹣ m+ n+2），

∴DF=﹣ m+ n+2﹣（ m2﹣ m+2）=﹣ m2+2m+ n，

∵OC∥DF，

∴∠OCB=∠FDB，

∵DE∥CA，

∴∠ACB=∠EDB，

∴∠OCA=∠FDE，

∴Rt△OCA∽Rt△FDE，

∴ = ，

∴ = = =2，

∴﹣ m2+2m+ n=2n，

∴n=﹣ m2+ m，

在Rt△DEF中，DE= = EF= n=﹣ m2+ m，

∵DE=﹣ （m﹣2）2+ ，

∴当m=2时，DE的长有最大值，最大值为 ；

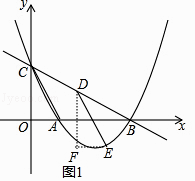
（3）

解：四边形CAED为菱形．理由如下：

AC= = ，BC= =2 ，

∵点D为BC的中点，

∴D（2，1），CD= ，

易得直线AC的解析式为y=﹣2x+2，

设直线DE的解析式为y=﹣2x+p，

把D（2，1）代入得1=﹣4+p，解得p=4，

∴直线DE的解析式为y=﹣2x+5，

解方程组 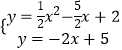得 或 ，则E（3，﹣1），

∴DE= = ，

∴AC=DE，

而AC∥DE，

∴四边形CAED为平行四边形，

∵CA=CD，

∴四边形CAED为菱形．

【解析】解：（1）当x=0时，y=kx+2=2，则C（0，2），
把C（0，2）代入y=a（x﹣1）（x﹣4）得a（﹣1）（﹣4）=2，解得a= ，
∴抛物线解析式为y= （x﹣1）（x﹣4），即y= x2﹣ x+2；
所以答案是y= x2﹣ x+2；
【考点精析】根据题目的已知条件，利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．