题目内容
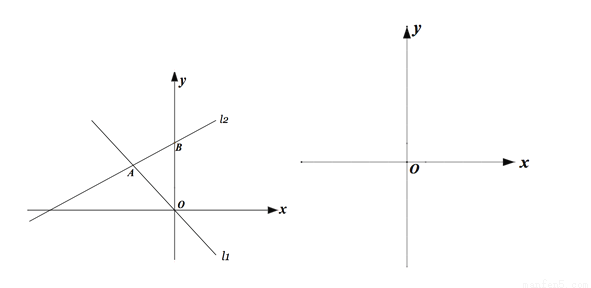
如图,在平面直角坐标系中,直线l1的解析式为y=-x,直线l2与l1交于A点(a,-a)与,与y轴交于点B(0,b),其中a,b满足(a+2)2+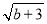 =0 .
=0 .
(1)求直线l2放入解析式;
(2)在平面直角坐标系中第二象限有一点P(m,5),使得S△AOP=S△AOB,请求出点P的坐标;
(3)已知平行于y轴且位于y轴左侧有一动直线,分别与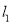 ,
, 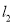 交于点M、N,且点M在点N的下方,点Q为y轴上一动点,且△MNQ为等腰直角三角形,请直接写出满足条件的点Q的坐标.
交于点M、N,且点M在点N的下方,点Q为y轴上一动点,且△MNQ为等腰直角三角形,请直接写出满足条件的点Q的坐标.
练习册系列答案
相关题目


 地驶向
地驶向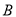 地,甲车比乙车早行驶
地,甲车比乙车早行驶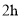 ,并且在途中休息了
,并且在途中休息了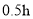 ,休息前后速度相同,如图是甲乙两车行驶的距离
,休息前后速度相同,如图是甲乙两车行驶的距离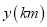 与时间
与时间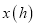 的函数图象,当甲车行驶__________
的函数图象,当甲车行驶__________ 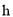 时,两车恰好相距
时,两车恰好相距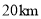 .
.
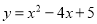 化成
化成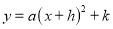 的形式应为__________.
的形式应为__________.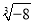 = .
= .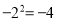 B.
B. 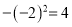 C.
C. 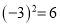 D.
D. 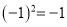
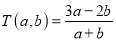 ,其中
,其中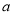 、
、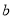 为实数,且
为实数,且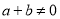 ”,比如:
”,比如: 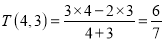 ,解关于m的不等式组
,解关于m的不等式组 ,则m的取值范围是_______.
,则m的取值范围是_______.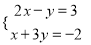
 ,并求其非负整数解.
,并求其非负整数解.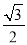 B.
B. 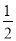 C.
C.  D.
D.