题目内容
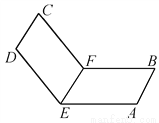
如图所示,取一张长方形的硬纸板ABCD,将硬纸板ABCD对折使CD与AB重合,EF为折痕.把长方形ABFE平放在桌面上,另一个面CDEF无论怎么改变位置总有CD∥AB存在,你知道为什么吗?
练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
题目内容
如图所示,取一张长方形的硬纸板ABCD,将硬纸板ABCD对折使CD与AB重合,EF为折痕.把长方形ABFE平放在桌面上,另一个面CDEF无论怎么改变位置总有CD∥AB存在,你知道为什么吗?

 名师点拨卷系列答案
名师点拨卷系列答案