题目内容
E是正方形ABCD内一点，且△EAB是等边三角形，则∠ADE的度数是
- A.70°
- B.72.5°
- C.75°
- D.77.5°
C
分析：根据等边三角形的性质可得到AE=AB，从而得到AD=AE，根据等边对等角及三角形的内角和定理即可求得∠ADE的度数．
解答：∵△EAB是等边三角形
∴∠DAE=90°-60°=30°，AE=AB
∴AD=AE
∴∠ADE=∠AED=
（180°-30°）=75°
故选C．
点评：本题考查了△ADE是等腰三角形的判定是解决本题的关键．
分析：根据等边三角形的性质可得到AE=AB，从而得到AD=AE，根据等边对等角及三角形的内角和定理即可求得∠ADE的度数．
解答：∵△EAB是等边三角形
∴∠DAE=90°-60°=30°，AE=AB
∴AD=AE
∴∠ADE=∠AED=
（180°-30°）=75°故选C．
点评：本题考查了△ADE是等腰三角形的判定是解决本题的关键．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
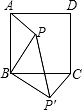如图，P是正方形ABCD内一点，将△ABP移到△CBP′位置，若BP=3，则PP′的长为
如图，点P是正方形ABCD内的一点，若PA=a，PB=2a，PC=3a，（a＞0），那么∠APB的大小是（ ）| A、100° | B、120° | C、135° | D、150° |
已知：如图，P是正方形ABCD内一点，∠APB=135°，BP=1，AP=
B与BC重合，连接PP′，得到△PBP′．
如图，点P是正方形ABCD内一点，连接AP、BP、CP、DP，若△ABP是等边三角形．