Question

射线QN与等边△ABC的两边AB，BC分别交于点M，N，且AC∥QN，AM=MB=2cm，QM=4cm．动点P从点Q出发，沿射线QN以每秒1cm的速度向右移动，经过t秒，以点P为圆心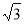，cm为半径的圆与△ABC的边相切（切点在边上），请写出t可取的一切值 （单位：秒）

 

 

Answer 1

t=2或3≤t≤7或t=8．

【解析】

试题分析：∵△ABC是等边三角形，

∴AB=AC=BC=AM+MB=4cm，∠A=∠C=∠B=60°，

∵QN∥AC，AM=BM．∴N为BC中点，∴MN=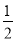AC=2cm，∠BMN=∠BNM=∠C=∠A=60°，

分为三种情况：①如图1，

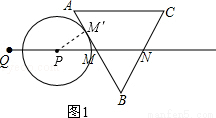
当⊙P切AB于M′时，连接PM′，则PM′=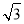cm，∠PM′M=90°，

∵∠PMM′=∠BMN=60°，∴M′M=1cm，PM=2MM′=2cm，∴QP=4cm﹣2cm=2cm，即t=2；

②如图2，

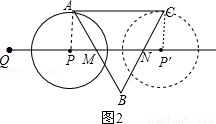
当⊙P于AC切于A点时，连接PA，则∠CAP=∠APM=90°，∠PMA=∠BMN=60°，AP=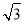cm，

∴PM=1cm，∴QP=4cm﹣1cm=3cm，

即t=3，

当⊙P于AC切于C点时，连接P′C，

则∠CP′N=∠ACP′=90°，∠P′NC=∠BNM=60°，CP′=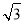cm，∴P′N=1cm，

∴QP=4cm+2cm+1cm=7cm，

即当3≤t≤7时，⊙P和AC边相切；

③如图3，

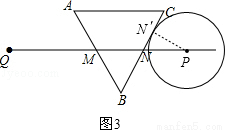
当⊙P切BC于N′时，连接PN′，则PN′=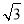cm，∠PN′N=90°，

∵∠PNN′=∠BNM=60°，∴N′N=1cm，PN=2NN′=2cm，∴QP=4cm+2cm+2cm=8cm，

即t=8；

故答案为：t=2或3≤t≤7或t=8．

考点：1．切线的性质；2．等边三角形的性质；3．分类讨论．