题目内容
已知tanα=
，那么sinα=
．（其中α为锐角）
| 4 |
| 3 |
| 4 |
| 5 |
| 4 |
| 5 |
分析：根据锐角三角函数的定义，设∠A=α，放在直角三角形ACB中，设BC=4x，AC=3x，由勾股定理求出AB，再根据锐角三角函数的定义求出即可．
解答：解：
∵∠C=90°，∠A=α，
∵tanα=
=
，
设BC=4x，AC=3x，
由勾股定理得：AB=
=5x，
∴sinα=sin∠A=
=
=
．
故答案为：
．
∵∠C=90°，∠A=α，
∵tanα=
| 4 |
| 3 |
| CB |
| AC |
设BC=4x，AC=3x，
由勾股定理得：AB=
| AC2+BC2 |
∴sinα=sin∠A=
| BC |
| AB |
| 4x |
| 5x |
| 4 |
| 5 |
故答案为：
| 4 |
| 5 |
点评：本题考查了勾股定理，锐角三角函数等知识点，解此题的关键是把所求角放在直角三角形中，思路是根据锐角三角函数的定义和直角三角形求出即可．题目较好，难度不大．
练习册系列答案
相关题目
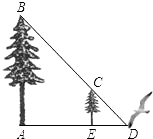如图，小鸟的妈妈在地面D处寻找到食物，准备飞到大树的顶端B处给非常饥饿的小鸟喂食，途中经过小树树顶C处，已知小树高为4米，大树与小树之间的距离为9米，已知tan∠BDA=
