Question

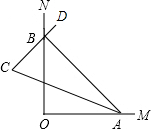如图，已知∠MON=90°，点A，B分别在射线OM，ON上移动，∠OAB的角平分线与∠ABO的外角平分线交于点C．
①当∠OAB=60°时，求∠ACB的度数；
②试猜想，随着点A，B的移动，∠ACB的度数是否变化？说明理由．

Answer 1

分析：根据三角形的一个外角等于和它不相邻的两个内角的和，∠OBF=∠OAB+∠MON，∠CBF=∠ACB+∠CAB，再根据角平分线的定义∠BAC=

1

2

∠OAB，∠CBF=

1

2

∠OBF，代入整理即可得到∠ACB=

1

2

∠MON=45°．

解答：解：①如图，延长AB到点F．
∵AC平分∠OAB（已知），
∴∠BAC=

1

2

∠OAB（角平分线的定义），
∵BC平分∠OBF（已知），
∴∠CBF=

1

2

∠OBD（角平分线定义），
∠OBF=∠MON+∠OAB（三角形的外角性质），∠CBF=∠ACB+∠BAC（三角形的外角性质），
∴∠ACB=∠CBF-∠BAC=

1

2

（∠MON+∠OAB）-

1

2

∠OAB=

1

2

∠MON=

1

2

×90°=45°，即∠ACB=45°；

②∠ACB的大小不变．
理由如下：由①知，∠ACB=∠CBF-∠BAC=

1

2

∠MON=45°．即∠ACB的度数是定值．

点评：本题主要考查三角形的一个外角等于和它不相邻的两个内角的和的性质以及角平分线的定义，熟练掌握性质和定义是解题的关键．