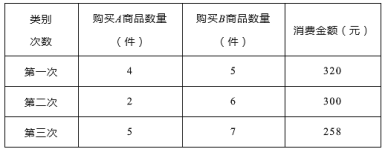
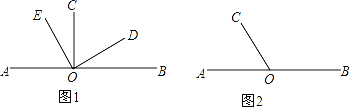题目内容
【题目】已知:平行四边形ABCD的两边AB,AD的长是关于x的方程x2﹣mx+![]() ﹣
﹣![]() =0的两个实数根.
=0的两个实数根.
(1)m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么ABCD的周长是多少?
【答案】(1)当m为1时,四边形ABCD是菱形,边长是![]() ;(2)ABCD的周长是5.
;(2)ABCD的周长是5.
【解析】
(1)根据菱形的性质可得出AB=AD,结合根的判别式,即可得出关于m的一元二次方程,解之即可得出m的值,将其代入原方程,解之即可得出菱形的边长;
(2)将x=2代入原方程可求出m的值,将m的值代入原方程结合根与系数的关系可求出方程的另一根AD的长,再根据平行四边形的周长公式即可求出ABCD的周长.
解:(1)∵四边形ABCD是菱形,
∴AB=AD.
又∵AB、AD的长是关于x的方程x2﹣mx+![]() ﹣
﹣![]() =0的两个实数根,
=0的两个实数根,
∴△=(﹣m)2﹣4×(![]() ﹣
﹣![]() )=(m﹣1)2=0,
)=(m﹣1)2=0,
∴m=1,
∴当m为1时,四边形ABCD是菱形.
当m=1时,原方程为x2﹣x+![]() =0,即(x﹣
=0,即(x﹣![]() )2=0,
)2=0,
解得:x1=x2=![]() ,
,
∴菱形ABCD的边长是![]() .
.
(2)把x=2代入原方程,得:4﹣2m+![]() ﹣
﹣![]() =0,
=0,
解得:m=![]() .
.
将m=![]() 代入原方程,得:x2﹣
代入原方程,得:x2﹣![]() x+1=0,
x+1=0,
∴方程的另一根AD=1÷2=![]() ,
,
∴ABCD的周长是2×(2+![]() )=5.
)=5.

【题目】某中学九(2)班同学为了了解2019年某小区家庭月均用水情况,随机调查了该小区的部分家庭,并将调查数据进行如下整理:
月均用水量 | 频数 | 频率 |
| 6 | 0.12 |
| ________ | 0.24 |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | ________ |
| 2 | 0.04 |

请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)月均用水量的中位数落在第________小组;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20吨的家庭大约有多少户?