题目内容
【题目】直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 是
是![]() 轴上一点,若将
轴上一点,若将![]() 沿
沿![]() 折叠,点
折叠,点![]() 恰好落在
恰好落在![]() 轴上,则点
轴上,则点![]() 的坐标为___________.
的坐标为___________.
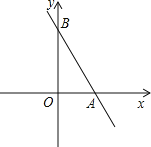
【答案】(0,![]() )或(0,-
)或(0,-![]() )
)
【解析】
设沿直线AM将△ABM折叠,点B正好落在x轴上的C点,则有AB=AC,而AB的长度根据已知可以求出,所以C点的坐标由此求出;又由于折叠得到CM=BM,在直角△CMO中根据勾股定理可以求出OM,也就求出M的坐标.注意分两种情况求解.
解:如图所示,当点M在y轴正半轴上时,设沿直线AM将△ABM折叠,点B正好落在x轴上的C点,则有AB=AC,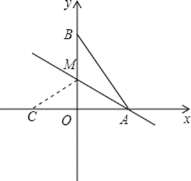
∵直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点A、B,
轴分别交于点A、B,
∴A(5,0),B(0,12),
又OA=5,OB=12,
∴AB=13,
∴点C的坐标为:(-8,0).
再设M点坐标为(0,b),
则CM=BM=12-b,
∵CM2=CO2+OM2,
∴b=![]() ,
,
∴M(0,![]() ),
),
如图所示,当点M在y轴负半轴上时,设OM=m,
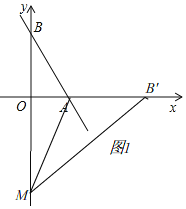
由折叠知,AB'=AB=13,B'M=BM,BM=OB+OM=12+m,
∴OB'=18,B'M=12+m
根据勾股定理得,![]() ,
,
∴m=![]() ,
,
∴M(0,-![]() )
)
故答案为:(0,![]() )或(0,-
)或(0,-![]() ).
).

练习册系列答案
相关题目