题目内容
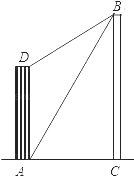
【题目】如图，以
的边
、
为边的等边三角
和等边三角形
，四边形
是平行四边形．
当
满足什么条件时，四边形是矩形；
当满足什么条件时，平行四边形不存在；
当分别满足什么条件时，平行四边形是菱形，正方形？
【答案】
当
时，四边形
是矩形； 
当
时平行四边形不存在，当
、时平行四边形是正方形．
【解析】
（1）根据矩形的四角相等为90度求解；
（2）根据D、A、E在同一条直线上时不能构成四边形求解；
（3）分别根据菱形的四边相等和正方形的四边相等，四角相等的特性解题．
当时，四边形是矩形，
∴
；
∵四边形是平行四边形，
∴四边形是矩形（有一个角是直角的平行四边形是矩形）；
当时平行四边形不存在，
；
当且
不等于
时平行四边形是菱形．
综上可知：当、时平行四边形是正方形．
练习册系列答案
一线名师提优试卷系列答案
相关题目
