题目内容
满足下列条件的△ABC,其中是直角三角形的有
①∠A=2∠B=3∠C;②∠A=∠B=30°;③∠A+∠B=∠C;④∠A= ∠B=
∠B= ∠C;⑤∠A+∠B=2∠C.
∠C;⑤∠A+∠B=2∠C.
- A.1个
- B.2个
- C.3个
- D.4个
B
分析:由一个三角形三角和为180°,分别计算出各个角的度数,而知道是否为直角三角形.
解答:①设∠C=x,则∠B= x,∠A=3x,则x+
x,∠A=3x,则x+ x+3x=180°,x=(32
x+3x=180°,x=(32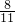 )°,3x≠90°,故不正确;
)°,3x≠90°,故不正确;
②∠A=∠B=30°,则∠C=180°-∠A-∠B=180°-30°-30°=120°,故错误;
③∠A+∠B=∠C,则2∠C=180°,∠C=90°,故正确;
④∠A= ∠B=
∠B= ∠C,则设∠A=x,则∠B=2x,∠C=3x,x+2x+3x=180°,x=30°,3x=3×30°=90°,故正确;
∠C,则设∠A=x,则∠B=2x,∠C=3x,x+2x+3x=180°,x=30°,3x=3×30°=90°,故正确;
⑤∠A+∠B=2∠C,则3∠C=180°,∠C=60°,∠A+∠B=60°,不能判定是直角三角形,故错误.
故选B.
点评:解答此类题目时一定要注意应用三角形的内角和定理.属较简单题目.
分析:由一个三角形三角和为180°,分别计算出各个角的度数,而知道是否为直角三角形.
解答:①设∠C=x,则∠B=
 x,∠A=3x,则x+
x,∠A=3x,则x+ x+3x=180°,x=(32
x+3x=180°,x=(32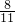 )°,3x≠90°,故不正确;
)°,3x≠90°,故不正确;②∠A=∠B=30°,则∠C=180°-∠A-∠B=180°-30°-30°=120°,故错误;
③∠A+∠B=∠C,则2∠C=180°,∠C=90°,故正确;
④∠A=
 ∠B=
∠B= ∠C,则设∠A=x,则∠B=2x,∠C=3x,x+2x+3x=180°,x=30°,3x=3×30°=90°,故正确;
∠C,则设∠A=x,则∠B=2x,∠C=3x,x+2x+3x=180°,x=30°,3x=3×30°=90°,故正确;⑤∠A+∠B=2∠C,则3∠C=180°,∠C=60°,∠A+∠B=60°,不能判定是直角三角形,故错误.
故选B.
点评:解答此类题目时一定要注意应用三角形的内角和定理.属较简单题目.

练习册系列答案
相关题目
满足下列条件的各对三角形中相似的两个三角形有( )
| A、∠A=60°,AB=5cm,AC=10cm;∠A′=60°,A′B′=3cm,A′C′=10cm | B、∠A=45°,AB=4cm,BC=6cm;∠D=45°,DE=2cm,DF=3cm | C、∠C=∠E=30°,AB=8cm,BC=4cm;DF=6cm,FE=3cm | D、∠A=∠A′,且AB•A′C′=AC•A′B′ |


 如图,△ABE≌△EDC,E在BD上,AB⊥BD,B为垂足.
如图,△ABE≌△EDC,E在BD上,AB⊥BD,B为垂足.