题目内容
如图所示，已知PA、PC分别是△ABC的外角∠DAC、∠ECA的平分线，PM⊥BD，PN⊥BE，垂足分别为M、N，那么PM与PN的关系是
- A.PM＞PN
- B.PM=PN
- C.PM＜PN
- D.无法确定
B
分析：利用外角平分线上的点到角两边的反向延长线的距离相等即可判断关系．
解答：
解：过点P作PH⊥AC，垂足为H，
∵PA、PC分别是△ABC的外角∠DAC、∠ECA的平分线，PM⊥BD，PN⊥BE，
∴PM=PH，PH=PN，
∴PM=PN
故选B．
点评：本题主要考查了外角平分线上的点到角两边的反向延长线的距离相等，作出辅助线是正确解答本题的关键．
分析：利用外角平分线上的点到角两边的反向延长线的距离相等即可判断关系．
解答：
解：过点P作PH⊥AC，垂足为H，∵PA、PC分别是△ABC的外角∠DAC、∠ECA的平分线，PM⊥BD，PN⊥BE，
∴PM=PH，PH=PN，
∴PM=PN
故选B．
点评：本题主要考查了外角平分线上的点到角两边的反向延长线的距离相等，作出辅助线是正确解答本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
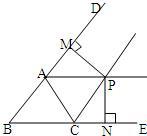14、如图所示，已知PA、PC分别是△ABC的外角∠DAC、∠ECA的平分线，PM⊥BD，PN⊥BE，垂足分别为M、N，那么PM与PN的关系是（ ）
，⊙O的半径等于3，则阴影部分的面积为________
