题目内容
1.如图,有一路灯杆AB,在灯光下,小明在点D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己的影长FG=4m,如果小明的身高为1.6m,则路灯杆AB的高度为6.4m.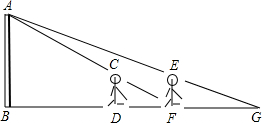
分析 根据相似三角形的判定与性质得出△ABF∽△CDF,△ABG∽△EFG,故$\frac{BD+DF}{DF}$=$\frac{BG}{FG}$,$\frac{AB}{EF}$=$\frac{BG}{FG}$,进而得出BD的长,即可得出AB的长.
解答 解:由题意可得:
△ABF∽△CDF,△ABG∽△EFG,
故$\frac{AB}{CD}$=$\frac{BD+DF}{DF}$,$\frac{AB}{EF}$=$\frac{BG}{FG}$,
∵DF=3m,FG=4m,EF=CD=1.6m,
则$\frac{BD+DF}{DF}$=$\frac{BG}{FG}$,
故$\frac{BD+3}{3}$=$\frac{BD+3+4}{4}$,
解得:BD=9,
故$\frac{AB}{1.6}$=$\frac{9+3}{3}$,
解得:AB=6.4,
答:路灯杆AB的高度为6.4m.
故答案为:6.4m.
点评 此题主要考查了相似三角形的应用,根据题意得出$\frac{BD+DF}{DF}$=$\frac{BG}{FG}$是解题关键.

练习册系列答案
相关题目
9.某药品原价每盒25元,在国家的医改政策的指导下,连续两次降价a%,后售价为每盒18元,下列方程正确的是( )
| A. | 25(1+a%)2=18 | B. | 25(1-a%)2=18 | C. | 25(1-2a%)=18 | D. | 25(1-a2%)=18 |
16.下列说法正确的是( )
| A. | 一个数不是整数就是负数 | B. | 整数和小数统称为有理数 | ||
| C. | 有理数中没有最小的非负整数 | D. | 0是正、负数的分界线 |
6.如图四个几何体:其中从左面看到的形状图与从上面看到的形状图相同的几何体共有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.下列各组数中不能作为直角三角形的三边长的是( )
| A. | 6,8,10 | B. | 7,24,25 | C. | 1.5,2,3 | D. | 9,12,15 |
 如图,正六边形ABCDEF的每一个外角的度数是60度.
如图,正六边形ABCDEF的每一个外角的度数是60度.