题目内容
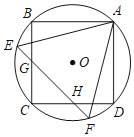
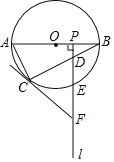
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 为
为![]() 上一点,点
上一点,点![]() 是半径
是半径![]() 上一动点(不与
上一动点(不与![]() ,
,![]() 重合),过点
重合),过点![]() 作射线
作射线![]() ,分别交弦
,分别交弦![]() ,
,![]() 于
于![]() ,
,![]() 两点,在射线
两点,在射线![]() 上取点
上取点![]() ,使
,使![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)当点![]() 是
是![]() 的中点时,
的中点时,
①若![]() ,判断以
,判断以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是什么特殊四边形,并说明理由;
为顶点的四边形是什么特殊四边形,并说明理由;
②若![]() ,且
,且![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)①四边形![]() 是菱形,理由见解析;②5.
是菱形,理由见解析;②5.
【解析】
(1)连接![]() ,利用
,利用![]() 和
和![]() 再进行等量代换证明OC⊥FC即可;
再进行等量代换证明OC⊥FC即可;
(2)①先证明![]() ,
,![]() 均为等边三角形,求得
均为等边三角形,求得![]() ,即可求解;
,即可求解;
②利用三角函数![]() ,和勾股定理求出AC,BC,再利用垂径定理求出HB,利用三角形面积公式求出PE,再求出OP,BP,DP即可.
,和勾股定理求出AC,BC,再利用垂径定理求出HB,利用三角形面积公式求出PE,再求出OP,BP,DP即可.
解:(1)证明:如图1,连接![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() 是
是![]() 的切线.
的切线.
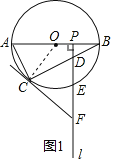
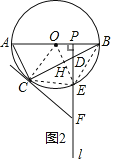
(2)如图2,连接![]() ,OE交CB于点H.
,OE交CB于点H.
①以![]() 为顶点的四边形是菱形.理由如下:
为顶点的四边形是菱形.理由如下:
![]() 是直径,
是直径,![]() ,
,
![]() ,
,![]() ,
,
![]() 点
点![]() 是
是![]() 的中点,
的中点,
![]() ,
,
![]()
![]() ,
,![]() 均为等边三角形,
均为等边三角形,
![]()
![]() 四边形
四边形![]() 是菱形;
是菱形;
②![]() ,设
,设![]() ,
,![]() ,
,
由勾股定理得![]() ,即
,即![]() ,解得
,解得![]() ,
,
![]() ,
,![]() ,
,
∵AB=20,
∴OE=OB=10,
![]() 点
点![]() 是
是![]() 的中点,
的中点,
![]() ,
,![]() ,
,
![]() ,即
,即![]() ,解得:
,解得:![]() ,
,
由勾股定理得![]() ,
,
![]() ,
,
![]() ,即
,即![]()
![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目