题目内容
某工厂以80元/箱的价格购进60箱原材料,准备由甲、乙两车间全部用于生产A产品.甲车间用每箱原材料可生产出A产品12千克,需耗水4吨;乙车间通过节能改造,用每箱原材料可生产出的A产品比甲车间少2千克,但耗水量是甲车间的一半.已知A产品售价为30元/千克,水价为5元/吨.如果要求这两车间生产这批产品的总耗水量不得超过200吨,那么该厂如何分配两车间的生产任务,才能使这次生产所能获取的利润w最大?最大利润是多少?(注:利润=产品总售价-购买原材料成本-水费)
解:设甲车间用x箱原材料生产A产品,则乙车间用(60-x)箱原材料生产A产品.
由题意得4x+2(60-x)≤200, 解得x≤40.
w=30[12x+10(60-x)]-80×60-5[4x+2(60-x)]=50x+12 600,
 ∵50>0,∴w随x的增大而增大.∴当x=40时,w取得最大值,为14 600元.
∵50>0,∴w随x的增大而增大.∴当x=40时,w取得最大值,为14 600元.
答:甲车间用40箱原材料生产A产品,乙车间用20箱原材料生产A产品,可使工厂所获利润最大,最大利润为14 600元.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目

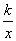 的图象经过点A(-1,4),直线y=-x + b(b≠0) 与双曲线y=
的图象经过点A(-1,4),直线y=-x + b(b≠0) 与双曲线y=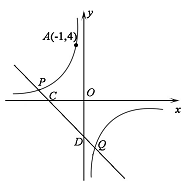

 B.
B. C.
C. D.
D.

 上任意一点,是过点(0,﹣2)且与x轴平行的直线,过点P作直线PH⊥l,垂足为H, PH交x轴于Q.
上任意一点,是过点(0,﹣2)且与x轴平行的直线,过点P作直线PH⊥l,垂足为H, PH交x轴于Q. ②如图2,已知线段AB=6,端点A,B在抛物线
②如图2,已知线段AB=6,端点A,B在抛物线 ,其中x=
,其中x=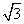 +
+ ,y=
,y=