题目内容
已知一元二次方程x2-2x+m=0.
(1)若方程有两个实数根,求m的范围;
(2)若方程的两个实数根为x1,x2,且x1+x2+x1x2=3,求m的值.
(1)若方程有两个实数根,求m的范围;
(2)若方程的两个实数根为x1,x2,且x1+x2+x1x2=3,求m的值.
考点:根的判别式,根与系数的关系
专题:计算题
分析:(1)根据判别式的意义得到△=(-2)2-4m≥0,然后解不等式即可;
(2)根据根与系数的关系得到x1+x2=2,x1x2=m,再由x1+x2+x1x2=3得到2+m=3,然后解一次方程即可.
(2)根据根与系数的关系得到x1+x2=2,x1x2=m,再由x1+x2+x1x2=3得到2+m=3,然后解一次方程即可.
解答:解:(1)根据题意得△=(-2)2-4m≥0,
解得m≤1;
(2)根据题意得x1+x2=2,x1x2=m,
∵x1+x2+x1x2=3,
∴2+m=3,
∴m=1.
解得m≤1;
(2)根据题意得x1+x2=2,x1x2=m,
∵x1+x2+x1x2=3,
∴2+m=3,
∴m=1.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了根与系数的关系.

练习册系列答案
相关题目
若代数式3axb2与代数式-a3by是同类项,则xy的值是( )
| A、9 | B、-9 | C、6 | D、-4 |
计算(-2)2012+(-2)2011的值为( )
| A、22011 |
| B、-22011 |
| C、-2 |
| D、2 |
某商店将某种服装先按成本提高60%标价,再以8折优惠卖出,结果每件服装仍可获利28元,则这种服装每件的成本价是( )
| A、240元 | B、100元 |
| C、120元 | D、95元 |
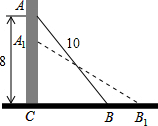 如果一个长为10m的梯子AB,斜靠在墙上,梯子的顶端距地面的垂直距离AC为8m.如果梯子的顶端A下滑1m到A1,请猜测梯子底端B滑动的1距离是否也会是1m?若不是,请求出滑动的距离.
如果一个长为10m的梯子AB,斜靠在墙上,梯子的顶端距地面的垂直距离AC为8m.如果梯子的顶端A下滑1m到A1,请猜测梯子底端B滑动的1距离是否也会是1m?若不是,请求出滑动的距离.