题目内容
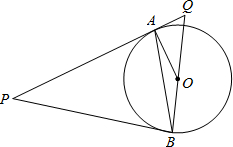
如图所示.P是⊙O外一点.PA是⊙O的切线.A是切点.B是⊙O上一点.且PA=PB,连接AO、BO、AB,并延长BO与切线PA相交于点Q.
(1)求证:PB是⊙O的切线;
(2)求证: AQ·PQ= OQ·BQ;
(3)设∠AOQ=![]() .若cos
.若cos![]() =
=![]() .OQ= 15.求AB的长
.OQ= 15.求AB的长


(1)证明:如图,连结OP
∵PA=PB,AO=BO,PO=PO
∴△APO≌△BPO ∴∠PBO=∠PAO=90°
∴PB是⊙O的切线
(2)证明:∵∠OAQ=∠PBQ=90°
∴△QPB∽![]() QOA
QOA
∴![]() 即AQ·PQ= OQ·BQ
即AQ·PQ= OQ·BQ
(3)解:cos![]() =
=![]() =
=![]() ∴AO=12
∴AO=12
∵△QPB∽![]() QOA ∠BPQ=∠AOQ=
QOA ∠BPQ=∠AOQ=![]()
∴tan∠BPQ=![]() =
=![]() ∴PB=36 PO=12
∴PB=36 PO=12![]()
∵![]() AB·PO= OB·BP ∴AB=
AB·PO= OB·BP ∴AB=![]()



练习册系列答案
相关题目
 =PB,连接AO、BO、AB,并延长BO与切线PA相交于点Q.
=PB,连接AO、BO、AB,并延长BO与切线PA相交于点Q.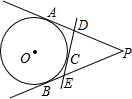 如图所示,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是
如图所示,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是
 如图所示,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是
如图所示,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是
 ,OQ=15,求AB的长.
,OQ=15,求AB的长.
 .若cos
.若cos .OQ= 15.求AB的长
.OQ= 15.求AB的长