题目内容
16. 如图,
如图,(1)写出△ABC关于x轴对称的△A1B1C1的各顶点的坐标;
(2)画出△ABC关于y轴对称的△A2B2C2;
(3)在y轴上求作一点P,使△PBC的周长最小.
分析 (1)首先写出点A,B,C的坐标,再根据过于x轴对称点的坐标特点即可得到△A1B1C1的各顶点的坐标;
(2)首先得到点A,B,C关于y轴对称点的坐标即可画出△ABC关于y轴对称的△A2B2C2;
(3)连接CB2,交y轴于点P,则此时△PBC的周长最小.
解答 解:
(1)△ABC关于x轴对称的△A1B1C1的各顶点坐标分别为:A1(-3,-2),B1(-4,3),C1(-1,1);
(2)如图1所示:
(3)如图2所示:
点评 本题考查的是作图-轴对称变换,熟知轴对称的性质是解答此题的关键.

练习册系列答案
相关题目
11.某学校计划购买A、B两种品牌的显示器共120台,A、B两种品牌显示器的单价分别为800元和1000元,设购买A品牌显示器x台,若学校购买这两种品牌显示器的总费用为110000元,那么A、B两种品牌的显示器各购买了多少台?根据题目信息完成上面的表格,并列出方程,列出的方程:800x+1000(120-x)=110000.
| 项目 品牌 | 单价/元 | 购买数量/台 | 购买费用/元 |
| A | 800 | x | 800x |
| B | 1000 | 120-x | 1000(120-x) |
9. 主持人主持节目时,站在舞台的黄金分割点处最自然得体.如图所示,如果舞台AB的长为12米,一名主持人现在站在A处,则她至少走( )米才最理想.
主持人主持节目时,站在舞台的黄金分割点处最自然得体.如图所示,如果舞台AB的长为12米,一名主持人现在站在A处,则她至少走( )米才最理想.
 主持人主持节目时,站在舞台的黄金分割点处最自然得体.如图所示,如果舞台AB的长为12米,一名主持人现在站在A处,则她至少走( )米才最理想.
主持人主持节目时,站在舞台的黄金分割点处最自然得体.如图所示,如果舞台AB的长为12米,一名主持人现在站在A处,则她至少走( )米才最理想.| A. | 18-6$\sqrt{5}$ | B. | 6$\sqrt{5}$-6 | C. | 6$\sqrt{5}$+6 | D. | 18-6$\sqrt{5}$或6$\sqrt{5}$-6 |
 已知如图,∠BOC与∠AOB互为补角,OD平分∠AOB,若∠COD=21°,求∠BOC的大小.
已知如图,∠BOC与∠AOB互为补角,OD平分∠AOB,若∠COD=21°,求∠BOC的大小.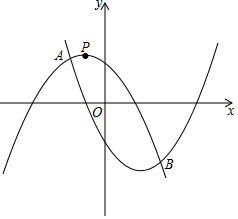 如图所示,抛物线y1=-ax2+(a-1)x+1经过点P(-$\frac{1}{3}$,$\frac{10}{9}$),且与抛物线y2=ax2-(a+1)x-1相交于A,B两点.
如图所示,抛物线y1=-ax2+(a-1)x+1经过点P(-$\frac{1}{3}$,$\frac{10}{9}$),且与抛物线y2=ax2-(a+1)x-1相交于A,B两点.