题目内容
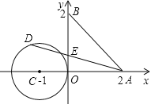
【题目】如图，已知A、B两点的坐标分别为（2，0）、（0，2），⊙C的圆心坐标为(﹣1，0)，半径为1．若D是⊙C上的一个动点，线段DA与y轴交于点E，则△ABE面积的最小值是（ ）
A. 2 B. 1 C. 
D. 
【答案】D
【解析】
由于OA的长为定值，若△ABE的面积最小，则BE的长最短，此时AD与⊙O相切；可连接CD．在Rt△ADC中，由勾股定理求得AD的长，易证得△AEO∽△ACD，根据相似三角形的性质可求出OE的长，进而可求出△ABE的面积．
若△ABE的面积最小，则AD与⊙C相切，连接CD，则CD⊥AD．
Rt△ACD中，CD＝1，AC＝OC+OA＝3．
由勾股定理，得：AD＝2
．
易证得△AOE∽△ADC，∴OE：OA=CD：AD，∴OE：2=1：2，解得：OE=
，∴S△ABE＝
BEOA
×（2
）×2
．
故选D．
练习册系列答案
相关题目
【题目】在“国学经典”主题比赛活动中，甲、乙、丙三位同学的三项比赛成绩如下表（单位：分）．
国学知识 | 现场写作 | 经典诵读 | |
甲 | 86 | 70 | 90 |
乙 | 86 | 80 | 90 |
丙 | 86 | 85 | 90 |
（1）若“国学知识”、“现场写作”“经典诵读”分别按30%，20%，50%的比例计入该同学的比赛得分，请分别计算甲、乙两位同学的得分；
（2）若甲同学的得分是80分，乙同学的得分是84分，则丙同学的得分是______分．
