题目内容
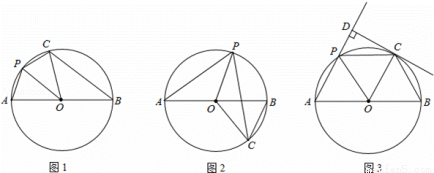
如图,正方形ABCD的边长为6,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为( )

A.4 B.
B.  C.
C. D.2
D.2
A
【解析】
试题分析:连接OC,
∵O为正方形ABCD的中心,
∴∠DCO=∠BCO,
又∵CF与CE都为圆O的切线,
∴CO平分∠ECF,即∠FCO=∠ECO,
∴∠DCO﹣∠FCO=∠BCO﹣∠ECO,即∠DCF=∠BCE,
又∵△BCE沿着CE折叠至△FCE,
∴∠BCE=∠ECF,
∴∠BCE=∠ECF=∠DCF= ∠BCD=30°,
∠BCD=30°,
在Rt△BCE中,设BE=x,则CE=2x,又BC=6,
根据勾股定理得:CE2=BC2+BE2,即4x2=x2+62,
解得:x=2 ,
,
∴CE=2x=4 .
.
故选:A.

考点: 1.切线的性质;2.翻折变换(折叠问题)

练习册系列答案
相关题目
 是等边三角形,点
是等边三角形,点 是△
是△ 按顺时针方向旋转后与△
按顺时针方向旋转后与△ 重合,则旋转中心是 ,最小旋转角等于 °
重合,则旋转中心是 ,最小旋转角等于 °

 ,AF=4
,AF=4 ,求AE的长.
,求AE的长.
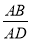 =
= 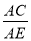 B.
B.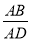 =
= 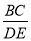 C.∠B=∠D D.∠C=∠AED
C.∠B=∠D D.∠C=∠AED
 的方程
的方程 .
. 取什么实数值,方程总有实数根;
取什么实数值,方程总有实数根; 、c恰好是这个方程的两个实数根,求△ABC的周长.
、c恰好是这个方程的两个实数根,求△ABC的周长.