Question

已知，AB是⊙O的直径，点P在弧AB上（不含点A、B），把△AOP沿OP对折，点A的对应点C恰好落在⊙O上．

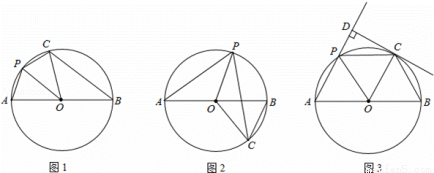
（1）当P、C都在AB上方时（如图1），判断PO与BC的位置关系（只回答结果）；

（2）当P在AB上方而C在AB下方时（如图2），（1）中结论还成立吗？证明你的结论；

（3）当P、C都在AB上方时（如图3），过C点作CD⊥直线AP于D，且CD是⊙O的切线，证明：AB=4PD．

 

Answer 1

见解析

【解析】

试题分析：（1）根据图形可知PO∥BC；（2）根据图形可知PO∥BC结论仍成立，根据条件只需要证明∠CPO=∠PCB即可；（3）根据条件证得△APO为等边三角形，进而得∠OCP=60°，CD是⊙O的切线，得∠OCD=90°,所以∠DCP=30°,所以PC=2PD,PC=AP=OA,所以AB=4PD.

试题解析：【解析】
（1）PO与BC的位置关系是PO∥BC；

（2）（1）中的结论PO∥BC成立，理由为：

由折叠可知：△APO≌△CPO，

∴∠APO=∠CPO， 又∵OA=OP，

∴∠A=∠APO， ∴∠A=∠CPO，

又∵∠A与∠PCB都为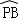所对的圆周角，

∴∠A=∠PCB， ∴∠CPO=∠PCB， ∴PO∥BC；

（3）∵CD为圆O的切线，

∴OC⊥CD，又AD⊥CD， ∴OC∥AD，

∴∠APO=∠COP， 由折叠可得：∠AOP=∠COP，

∴∠APO=∠AOP， 又OA=OP，∴∠A=∠APO，

∴∠A=∠APO=∠AOP， ∴△APO为等边三角形，

∴∠AOP=60°， 又∵OP∥BC，∴∠OBC=∠AOP=60°，又OC=OB，

∴△BCO为等边三角形，∴∠COB=60°，

∴∠POC=180°﹣（∠AOP+∠COB）=60°，又OP=OC，∴△POC也为等边三角形，

∴∠PCO=60°，PC=OP=OC， 又∵∠OCD=90°，∴∠PCD=30°，

在Rt△PCD中，PD=PC，

又∵PC=OP=AB，∴PD=AB，即AB=4PD．

考点：1.全等三角形的性质与判定；2.圆周角定理；3.切线的性质；4. 等边三角形的判定与性质.