题目内容
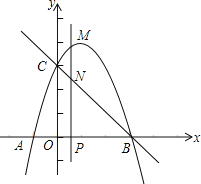
【题目】已知实数a、b、c满足(a-b)2=ab=c,有下列结论:①当c≠0时,![]() =3;②当c=5时,a+b=5:③当a、b、c中有两个相等时,c=0;④二次函数y=x2+bx-c与一次函数y=ax+1的图象有2个交点.其中正确的有_______
=3;②当c=5时,a+b=5:③当a、b、c中有两个相等时,c=0;④二次函数y=x2+bx-c与一次函数y=ax+1的图象有2个交点.其中正确的有_______
【答案】①④
【解析】
按照字母满足的条件,逐一分析计算得出答案即可.
解:①:∵(a-b)=ab,
∴a+b=3ab,对等式两边同时除以ab(ab≠0),∴![]() =3,此①正确;
=3,此①正确;
②:当c=5时,ab=c=5,(a-b)=c=5
又由公式:(a+b)=(a-b)+4ab得:
(a+b)=5+4×5=25,∴a+b=±5,故②错误;
③:当a=c,b=1时,即(a-1)=a,解得a=c=![]() ≠0,故③错误;
≠0,故③错误;
④:联立二次函数与一次函数解析式,得到:
x2+bx-c=ax+1,整理得:x2+(b-a)x-c-1=0,
△=(b-a)2-4×1×(-c-1)=c+4c+4=5c+4
∵(a-b)2总是大于等于0
∴(a-b)2=c≥0
∴5c≥0
∴5c+4≥4
故△=5c+4≥4>0,∴它们的图像总有2个交点,故④正确.
故答案为:①④.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
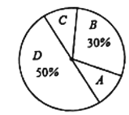
普通高中同步练习册系列答案【题目】研究机构对本地区18-20岁的大学生就某个问题做随机调查,要求被调查者从A、B、C、D四个选项中选择自己赞同的一项,并将结果绘制成两幅不完整的统计图(如图):
大学生就某个问题调查结果统计表 | 大学生就某个问题调查结果扇形统计图 | ||||||||||||
|
|
请结合图中信息解答以下问题:
(1)m=_____,b=_____.
(2)若该地区18~20岁的大学生有1.2万人,请估计这些大学生中选择赞同A选项的人数:
(3)该研究机构决定从选择“C”的人中随机抽取2名进行访谈,而选择“C”的这4人中只有一名男性,求这名男性刚好被抽取到的概率.