题目内容
如图，在边长为c的正方形中，有四个斜边为c的全等直角三角形，已知其直角边长为a，b．利用这
个图试说明勾股定理？
大正方形的面积可以表示为________
又可以表示为________
所以有________．
c2 （a-b）2+2ab a2+b2=c2
分析：根据大正方形的面积等于边长的平方解答；
还可以根据四个全等直角三角形的面积加上中间空白正方形的面积表示；
根据完全平方公式整理即可得解．
解答：大正方形的面积为：c2；
四个全等三角形的面积为：4×
×ab=2ab，
中间空白正方形的面积为：（a-b）2，
∴又可以表示为：（a-b）2+2ab；
∵（a-b）2+2ab=a2-2ab+b2+2ab=a2+b2，
∴a2+b2=c2．
故答案为：c2；（a-b）2+2ab；a2+b2=c2．
点评：本题考查了勾股定理的几何解释，利用不同的方法表示出大正方形的面积是解题的关键．
分析：根据大正方形的面积等于边长的平方解答；
还可以根据四个全等直角三角形的面积加上中间空白正方形的面积表示；
根据完全平方公式整理即可得解．
解答：大正方形的面积为：c2；
四个全等三角形的面积为：4×
×ab=2ab，中间空白正方形的面积为：（a-b）2，
∴又可以表示为：（a-b）2+2ab；
∵（a-b）2+2ab=a2-2ab+b2+2ab=a2+b2，
∴a2+b2=c2．
故答案为：c2；（a-b）2+2ab；a2+b2=c2．
点评：本题考查了勾股定理的几何解释，利用不同的方法表示出大正方形的面积是解题的关键．
练习册系列答案
相关题目
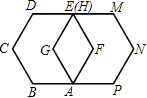如图，如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合，那么点B的对应点是点
已知：如图，在边长为a的正△ABC中，分别以A，B，C点为圆心，
如图，将边长为3的正六边形A1A2A3A4A5A6，在直线l上由图1的位置按顺时针方向向右作无滑动滚动，当A1第一次滚动到图2位置时，顶点A1所经过的路径的长为（ ）
已知：如图，在边长为a的正△ABC中，分别以A，B，C点为圆心，
长为半径作
，
，
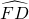，求阴影部分的面积．
长为半径作
，
，
，求阴影部分的面积．