题目内容
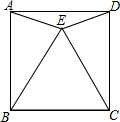
如图，正方形ABCD中有一点P，边长为4，且△PBC是等边三角形，则∠APD=______，
S△APD=______．
S△APD=______．
作PM⊥AD，PN⊥BC，
∵△BCP为等边三角形，∴∠PBC=60°，AB=BP，
∵正方形ABCD中∠ABC=90°，
∴∠ABP=30°∴∠BAP=75°，
∴∠DAP=15°，同理∠ADP=15°，
故∠APD=150°．
因为△BCP为等边三角形，所以M、N、P在一条直线上，
故MP=MN-PN，且MN=AB，
PN=
×4=2
，
故PM=4-2
，
S△APD=
×4×（4-2
）=8-4
．
故答案为 150°，8-4
．
∵△BCP为等边三角形，∴∠PBC=60°，AB=BP，
∵正方形ABCD中∠ABC=90°，
∴∠ABP=30°∴∠BAP=75°，
∴∠DAP=15°，同理∠ADP=15°，
故∠APD=150°．
因为△BCP为等边三角形，所以M、N、P在一条直线上，
故MP=MN-PN，且MN=AB，
PN=
| ||
| 2 |
| 3 |
故PM=4-2
| 3 |
S△APD=
| 1 |
| 2 |
| 3 |
| 3 |
故答案为 150°，8-4
| 3 |
练习册系列答案
阅读快车系列答案
相关题目
