题目内容
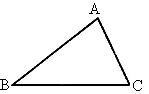
已知,锐角三角形ABC的三边AB=6cm,BC=7cm,AC=8cm,∠A=α,则△ABC的面积等于分析:过B点作BD⊥AC垂足为D,在三角形ABD中,根据三角函数的定义求出BD的长,然后根据三角形面积公式进行解答.
解答: 解:过B点作BD⊥AC垂足为D,
解:过B点作BD⊥AC垂足为D,
在Rt△ABD中,
∵sinα=
,
∴BD=6sinα,
∴S△ABC=
AC•BD=24sinα,
故答案为24sinα.
 解:过B点作BD⊥AC垂足为D,
解:过B点作BD⊥AC垂足为D,在Rt△ABD中,
∵sinα=
| BD |
| AB |
∴BD=6sinα,
∴S△ABC=
| 1 |
| 2 |
故答案为24sinα.
点评:本题主要考查三角形面积的知识点,熟记三角形的面积公式是解答本题的关键.

练习册系列答案
相关题目
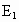 ,过点
,过点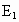 作
作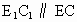 ,交OA于点
,交OA于点 ,作
,作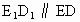 ,交OB于点
,交OB于点 .
. ,则
,则 是△AOB的内接三角形.
是△AOB的内接三角形.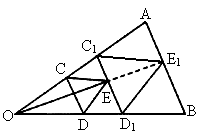
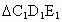 是等边三角形.
是等边三角形.
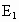 ,过点
,过点 作
作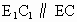 ,交OA于点
,交OA于点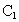 ,作
,作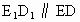 ,交OB于点
,交OB于点 .
.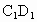 ,则
,则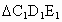 是△AOB的内接三角形.
是△AOB的内接三角形.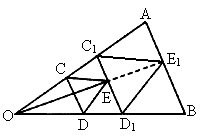
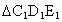 是等边三角形.
是等边三角形.