题目内容
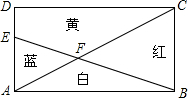如图，矩形广场ABCD，AB=4m，BC=3m，E是AD边上一点，AE=2m，AC、BE交于F，把广场分为四部分，这四部分分别由红、黄、蓝、白四种颜色的地砖铺成，四种颜色的地砖位置如图所示，求红、黄、蓝、白四部分面积是多少平方米？
分析：根据题中条件和三角形面积公式可求得：S△ABE=4，根据△AEF∽△CBF，EF：BF=AE：BC=2：3，可求得S△AEF=
，S△ABF=
，根据相似比可求出S△CBF=
，而四边形EFCD的面积为S四边形EFCD=S矩形ABCD-S△AEF-S△ABF-S△CBF=
平方米．
| 8 |
| 5 |
| 12 |
| 5 |
| 18 |
| 5 |
| 22 |
| 5 |
解答：解：如图，在矩形ABCD中，AD∥BC，
∴∠EAF=∠BCF，∠EFA=∠BFC，
∴△AEF∽△CBF，（2分）
∴
=
=
，
∵S△ABE=
AE•AB=
×2×4=4m2，（1分）
即S△ABF+S△AEF=4，
又∵
=
，（1分）
∴S△AEF=
，S△ABF=
，（2分）
∵
=(
)2=
，
∴S△CBF=
，（1分）
∴S四边形EFCD=S矩形ABCD-S△AEF-S△ABF-S△CBF=12-
-
-
=
m2．（1分）
答：红、黄、蓝、白四部分面积各是
平方米，
平方米，
平方米，
平方米．
∴∠EAF=∠BCF，∠EFA=∠BFC，
∴△AEF∽△CBF，（2分）
∴
| EF |
| BF |
| AE |
| BC |
| 2 |
| 3 |
∵S△ABE=
| 1 |
| 2 |
| 1 |
| 2 |
即S△ABF+S△AEF=4，
又∵
| S△AEF |
| S△ABF |
| 2 |
| 3 |
∴S△AEF=
| 8 |
| 5 |
| 12 |
| 5 |
∵
| S△AEF |
| S△CBF |
| AE |
| BC |
| 9 |
| 4 |
∴S△CBF=
| 18 |
| 5 |
∴S四边形EFCD=S矩形ABCD-S△AEF-S△ABF-S△CBF=12-
| 8 |
| 5 |
| 12 |
| 5 |
| 18 |
| 5 |
| 22 |
| 5 |
答：红、黄、蓝、白四部分面积各是
| 18 |
| 5 |
| 22 |
| 5 |
| 8 |
| 5 |
| 12 |
| 5 |
点评：主要考查了矩形的性质和相似三角形的性质．会利用三角形相似中的相似比来求算相关的线段和三角形的面积之间的关系是解题的关键．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
（2013•潍坊）为了改善市民的生活环境，我市在某河滨空地处修建一个如图所示的休闲文化广场，在Rt△ABC内修建矩形水池DEFG，使定点D，E在斜边AB上，F，G分别在直角边
为了改善市民的生活环境，我市在某河滨空地处修建一个如图所示的休闲文化广场，在Rt△ABC内修建矩形水池DEFG，使定点D，E在斜边AB上，F，G分别在直角边
米，∠BAC=60°，设EF=x米，DE=y米．
？
米，∠BAC=600.设EF=x米，DE=y米.
？
为了改善市民的生活环境，我市在某河滨空地处修建一个如图所示的休闲文化广场，在Rt△ABC内修建矩形水池DEFG，使定点D，E在斜边AB上，F，G分别在直角边
米，∠BAC=60°，设EF=x米，DE=y米．
？
米，∠BAC=600.设EF=x米，DE=y米.
？