题目内容
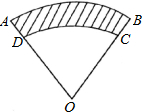
 如图,扇形的圆心角∠AOB=135°,C为扇形的弧上一点,∠BOC=45°,设扇形BOC、△AOC、弓形AmC的面积分别为S1、S2、S3,则它们之间的大小关系是________.(用“<”表示)
如图,扇形的圆心角∠AOB=135°,C为扇形的弧上一点,∠BOC=45°,设扇形BOC、△AOC、弓形AmC的面积分别为S1、S2、S3,则它们之间的大小关系是________.(用“<”表示)
S1<S3<S2
分析:设圆的半径为r,分别计算S1、S2、S3的面积后比较即可得到正确的答案.
解答:设圆的半径为r,
∵∠AOB=135°,∠BOC=45°,
∴∠AOC=90°,
∴S3= =
=
S2= r2
r2
S1=S扇形AOC-S2= -
- r2
r2
= r2,
r2,
∴S1<S3<S2.
故答案为S1<S3<S2.
点评:本题考查了扇形的面积的计算方法及等腰直角三角形的知识,解题的关键是正确的设出扇形的半径并利用扇形及弓形的面积求得其面积.
分析:设圆的半径为r,分别计算S1、S2、S3的面积后比较即可得到正确的答案.
解答:设圆的半径为r,
∵∠AOB=135°,∠BOC=45°,
∴∠AOC=90°,
∴S3=
 =
=
S2=
 r2
r2S1=S扇形AOC-S2=
 -
- r2
r2=
 r2,
r2,∴S1<S3<S2.
故答案为S1<S3<S2.
点评:本题考查了扇形的面积的计算方法及等腰直角三角形的知识,解题的关键是正确的设出扇形的半径并利用扇形及弓形的面积求得其面积.

练习册系列答案
相关题目
 如图,扇形的圆心角∠AOB=60°,AD=3cm,弧CD的长为3πcm,则图中阴影部分的面积为( )
如图,扇形的圆心角∠AOB=60°,AD=3cm,弧CD的长为3πcm,则图中阴影部分的面积为( )A、
| ||
B、
| ||
C、
| ||
| D、12πcm2 |
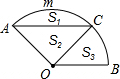 如图,扇形的圆心角∠AOB=135°,C为扇形的弧上一点,∠BOC=45°,设扇形BOC、△AOC、弓形AmC的面积分别为S1、S2、S3,则它们之间的大小关系是
如图,扇形的圆心角∠AOB=135°,C为扇形的弧上一点,∠BOC=45°,设扇形BOC、△AOC、弓形AmC的面积分别为S1、S2、S3,则它们之间的大小关系是
 。其中正确的有 (请写序号,少选,错选均不得分)
。其中正确的有 (请写序号,少选,错选均不得分) ,扇形
,扇形 的圆心角
的圆心角 ,点
,点 是
是 上异于
上异于 的动点,过点
的动点,过点 于
于 ,作
,作 于
于 ,连接
,连接 ,点
,点 在线段
在线段 ,连接
,连接 。当点
。当点 中,长度不变的是
中,长度不变的是 ;
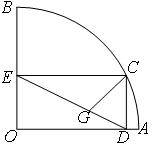
; ,正方形纸片
,正方形纸片 的边长为
的边长为 ,⊙
,⊙ 的半径为
的半径为 于点
于点 重合,且
重合,且 切⊙
切⊙ 交
交 边于点
边于点 的长为
的长为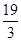 ;③已知
;③已知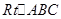 中,
中, ,则其内心和外心之间的距离是
,则其内心和外心之间的距离是 。其中正确的有 (请写序号,少选,错选均不得分)
。其中正确的有 (请写序号,少选,错选均不得分)

 的圆心角
的圆心角 ,点
,点 是
是 上异于
上异于 的动点,过点
的动点,过点 于
于 ,作
,作 于
于 ,连接
,连接 ,点
,点 在线段
在线段 ,连接
,连接 。当点
。当点 中,长度不变的是
中,长度不变的是 ;
;

 的边长为
的边长为 ,⊙
,⊙ 的半径为
的半径为 ,圆心
,圆心 于点
于点 重合,且
重合,且 切⊙
切⊙ 交
交 边于点
边于点 的长为
的长为 ;
; 中,
中, ,则其内心和外心之间的距离是
,则其内心和外心之间的距离是 。其中正确的有 (请写序号,少选,错选均不得分)
。其中正确的有 (请写序号,少选,错选均不得分)