题目内容
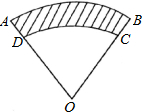 如图,扇形的圆心角∠AOB=60°,AD=3cm,弧CD的长为3πcm,则图中阴影部分的面积为( )
如图,扇形的圆心角∠AOB=60°,AD=3cm,弧CD的长为3πcm,则图中阴影部分的面积为( )A、
| ||
B、
| ||
C、
| ||
| D、12πcm2 |
分析:先利用弧长公式求出OD的长,再让大扇形面积减小扇形面积即可.
解答:解:∠DOC=60°,
CD=3π=
,解得R=9(cm),
OA=9+3=12(cm),
S扇形OAB-S扇形OCD=
=
=
π(cm2).
故选C.
CD=3π=
| 60πR |
| 180 |
OA=9+3=12(cm),
S扇形OAB-S扇形OCD=
| π60(122-92) |
| 360 |
| π×21×3 |
| 6 |
| 21 |
| 2 |
故选C.
点评:本题考查的是扇形面积的计算,利用扇形面积公式分别求出两个扇形的面积,然后相减求出阴影部分的面积.此题的关键是利用弧长公式求出OD.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
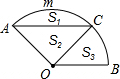 如图,扇形的圆心角∠AOB=135°,C为扇形的弧上一点,∠BOC=45°,设扇形BOC、△AOC、弓形AmC的面积分别为S1、S2、S3,则它们之间的大小关系是
如图,扇形的圆心角∠AOB=135°,C为扇形的弧上一点,∠BOC=45°,设扇形BOC、△AOC、弓形AmC的面积分别为S1、S2、S3,则它们之间的大小关系是
 。其中正确的有 (请写序号,少选,错选均不得分)
。其中正确的有 (请写序号,少选,错选均不得分) ,扇形
,扇形 的圆心角
的圆心角 ,点
,点 是
是 上异于
上异于 的动点,过点
的动点,过点 于
于 ,作
,作 于
于 ,连接
,连接 ,点
,点 在线段
在线段 ,连接
,连接 。当点
。当点 中,长度不变的是
中,长度不变的是 ;
; ,正方形纸片
,正方形纸片 的边长为
的边长为 ,⊙
,⊙ 的半径为
的半径为 于点
于点 重合,且
重合,且 切⊙
切⊙ 交
交 边于点
边于点 的长为
的长为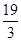 ;③已知
;③已知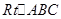 中,
中, ,则其内心和外心之间的距离是
,则其内心和外心之间的距离是 。其中正确的有 (请写序号,少选,错选均不得分)
。其中正确的有 (请写序号,少选,错选均不得分)

 的圆心角
的圆心角 ,点
,点 是
是 上异于
上异于 的动点,过点
的动点,过点 于
于 ,作
,作 于
于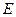 ,连接
,连接 ,点
,点 在线段
在线段 ,连接
,连接 。当点
。当点 中,长度不变的是
中,长度不变的是 ;
;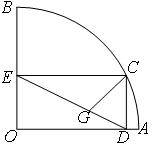

 的边长为
的边长为 ,⊙
,⊙ 的半径为
的半径为 ,圆心
,圆心 于点
于点 重合,且
重合,且 切⊙
切⊙ 交
交 边于点
边于点 的长为
的长为 ;
; 中,
中, ,则其内心和外心之间的距离是
,则其内心和外心之间的距离是 。其中正确的有 (请写序号,少选,错选均不得分)
。其中正确的有 (请写序号,少选,错选均不得分)