题目内容
如图，已知在平行四边形ABCD中，DE⊥AB，DF⊥BC，∠EDF=135°，则平行四边形的各角为________．
∠BAD=∠BCD=135°，∠B=∠ADC=45°
分析：根据四边形内角和为360°，由已知易求∠B=45°；再根据平行四边形的性质即可求出平行四边形的各角度数．
解答：∠E=∠F=90°，∠B+∠E+∠EDF+∠F=360°，
所以∠B+∠EDF=180°，
所以∠B=45°，
所以∠BAD=∠DCB=135°，∠ADC=45°．
故答案为：∠BAD=∠BCD=135°，∠B=∠ADC=45°．
点评：此题考查了平行四边形的性质和四边形的内角和为360°的性质，难度不大．
分析：根据四边形内角和为360°，由已知易求∠B=45°；再根据平行四边形的性质即可求出平行四边形的各角度数．
解答：∠E=∠F=90°，∠B+∠E+∠EDF+∠F=360°，
所以∠B+∠EDF=180°，
所以∠B=45°，
所以∠BAD=∠DCB=135°，∠ADC=45°．
故答案为：∠BAD=∠BCD=135°，∠B=∠ADC=45°．
点评：此题考查了平行四边形的性质和四边形的内角和为360°的性质，难度不大．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
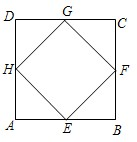四个顶点都在正方形边上的四边形叫做正方形的内接四边形．如图，四边形EFGH是正方形ABCD的内接平行四边形，且已知正方形ABCD的边长为4．
，BO＝AO．又∵AG⊥EB，∠1＋∠3＝
＝∠2＋∠3∴∠1＝∠2，∴Rt△BOE≌Rt△AOF解答此题后某同学产生了如下猜想：对上述命题，若点E在AC的延长线上，AG⊥EB，AG交EB的延长线于G，AG的延长线交DB的延长线于F，其它条件不变，如图，则仍有OE＝OF．问猜想所得的结论是否成立，请说明理由．
