Question

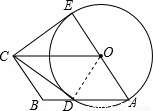
如图，四边形OABC是平行四边形，以O为圆心，OA为半径的圆交AB于D，延长AO交⊙O于E，连接CD，CE，若CE是⊙O的切线，解答下列问题：

（1）求证：CD是⊙O的切线；

（2）若BC=3，CD=4，求平行四边形OABC的面积．

 

 

Answer 1

（1)证明见解析；

（2）平行四边形OABC的面积S=12

【解析】

试题分析：（1）连接OD，求出∠EOC=∠DOC，根据SAS推出△EOC≌△DOC，推出∠ODC=∠OEC=90°，根据切线的判定推出即可；

（2）根据全等三角形的性质求出CE=CD=4，根据平行四边形性质求出OA=3，根据平行四边形的面积公式求出即可．

试题解析：（1）连接OD，

∵OD=OA，

∴∠ODA=∠A，

∵四边形OABC是平行四边形，

∴OC∥AB，

∴∠EOC=∠A，∠COD=∠ODA，

∴∠EOC=∠DOC，

又∵OE=OD，OC=OC，

∴△EOC≌△DOC（SAS），

∴∠ODC=∠OEC=90°，

即OD⊥DC，

∴CD是⊙O的切线；

（2）∵△EOC≌△DOC，

∴CE=CD=4，

∵四边形OABC是平行四边形，

∴OA=BC=3，

∴平行四边形OABC的面积S=OA×CE=3×4=12．

考点：1、全等三角形的性质和判定；2、切线的判定与性质；3、平行四边形的性质．