题目内容
如图，在四边形ABCD中，∠ABC＋∠DCB＝90°，E、F分别是AD、BC的中点，分别以AB、CD为直径作半圆，这两个半圆面积的和为8π，则EF的长为 （ ）
A．10 B．8 C．6 D．4
D．
【解析】
试题分析：连接BD，取BD的中点M，连接EM、FM，延长EM交BC于N，
∵∠ABC+∠C=360°﹣270°=90°，
∵E、F、M分别是AD、BC、BD的中点，∴EM=
AB，FM=
CD，EM∥AB，FM∥CD，
∴∠ABC=∠ENC，∠MFN=∠C，∴∠MNF+∠MFN=90°，
∴∠NMF=180°﹣90°=90°，∴∠EMF=90°，
由勾股定理得：
，
∴阴影部分的面积是：
=8π，∴EF=4，故选D．
考点：1．勾股定理；2．直角三角形斜边上的中线．
练习册系列答案
相关题目
+x2=0
，求OD的长．
米 C．
米 D．10米
；
；
……，
_______，
.
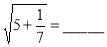