Question

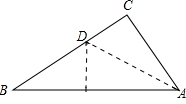如图，直角三角形纸片ABC中，AC=3，BC=4，折叠纸片使边AC落在斜边AB上，折痕为AD，则CD的长为（　　）

• A．2
• B．

  3

  2

• C．

  4

  3

• D．1

Answer 1

分析：首先根据勾股定理计算出AB的长，再根据折叠可得AC=AE=3，CD=DE，BE=5-3=2，然后设CD=DE=x，则BD=4-x，再在直角△BDE中利用勾股定理即可算出x的值．

解答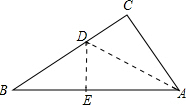：解：在直角△ABC中：AB=

AC2+BC2

=

9+16

=5，
根据折叠可得AC=AE=3，CD=DE，BE=5-3=2，
设CD=DE=x，则BD=4-x，
在直角△BDE中：（4-x）²=x²+2²，
解得：x=

3

2

．
故选：B．

点评：此题主要考查了图形的翻折变换，解题时，我们常常设要求的线段长为x，然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度，选择适当的直角三角形，运用勾股定理列出方程求出答案．我们运用方程解决时，应认真审题，设出正确的未知数．